Algosim 3.1 introduction
I have published a video showcasing version 3.1 of Algosim:
The video can also be watched on YouTube.
I have published a video showcasing version 3.1 of Algosim:
The video can also be watched on YouTube.
As a second example of plotting parameterised surfaces, let’s make an animated umbilic torus.
Unlike the Möbius strip, the umbilic torus divides ℝ3 into two parts – there’s an “inside” and an “outside”. Also unlike the Möbius strip, it is a two-sided surface, although only the external face is visible from the outside. Similar to the Möbius strip, it has a single “edge”, but whereas the edge of the Möbius strip goes two times around the z axis, the edge of the umbilic torus goes three times around it.
The camera in the animation above rotates about the z axis at the same angular rate as a highlighted u = const parameter curve. A single point on this parameter curve is indicated by a yellow ball; this ball moves along the single edge of the torus, so it goes three times around the z axis before it returns to its original position.
An inset shows the parameter-plane coordinates of the ball’s position.
Notice that each u = const parameter curve – and therefore the cross section of the torus – is a deltoid.
Full source:
F ≔ (u, v) ↦
❨
sin(u) ⋅ (7 + cos(u/3 − 2⋅v) + 2⋅cos(u/3 + v)),
cos(u) ⋅ (7 + cos(u/3 − 2⋅v) + 2⋅cos(u/3 + v)),
sin(u/3 − 2⋅v) + 2⋅sin(u/3 + v)
❩;
ForEach('(false, true), Opaque, (
S ≔ ClearScene("Umbilic torus");
T ≔ surf([−π, π] × [−π, π] @ F);
B ≔ sphere();
AdjustVisual(S,
"window width": 1080,
"window height": 1080);
AdjustVisual(S.axes, "grid count": 0);
AdjustVisual(T,
"unisided": true,
"show parameter curves": true,
"line width": .5,
"show surface": Opaque);
AdjustVisual(B,
"color": "yellow",
"radius": .2);
t ≔ 0.0;
u ≔ 0;
v ≔ 0;
Γ ≔ curve([−π, π] @ (s ↦ F(t, s)));
Π ≔ ClearDiagram("Parameter plane");
AdjustVisual(Π.view,
"xmin": −π,
"xmax": π,
"ymin": −π,
"ymax": π);
AdjustVisual(Π,
"auto normalize": true,
"window width": 300,
"window height": 300);
D ≔ disk(❨0, 0❩, 0.1);
scene("Umbilic torus");
repeat(
AdjustVisual(S.view, "rθφ": ❨28, π/4 − .75⋅π/4⋅sin(t/3)^5, π/4 − t❩);
Γ2 ≔ Γ; Γ ≔ curve([−π, π] @ (s ↦ F(t, s))); RemoveVisual(Γ2);
AdjustVisual(Γ,
"line width": 10,
"color": "black");
AdjustVisual(B, "position": F(u, v));
AdjustVisual(D, "position": ❨u, v❩);
t ≔ t + 0.02;
u ≔ u + 0.02;
if(u > π, (u ≔ u − 2⋅π; v ≔ v + 2⋅π/3));
if(v > π, (v ≔ v − 2⋅π));
sleep(0.01);
if(t > 3⋅2⋅π, break());
)
));
As a simple example of 3D visualisation in Algosim 3.1, let’s draw a Möbius strip and a normal vector field on it.
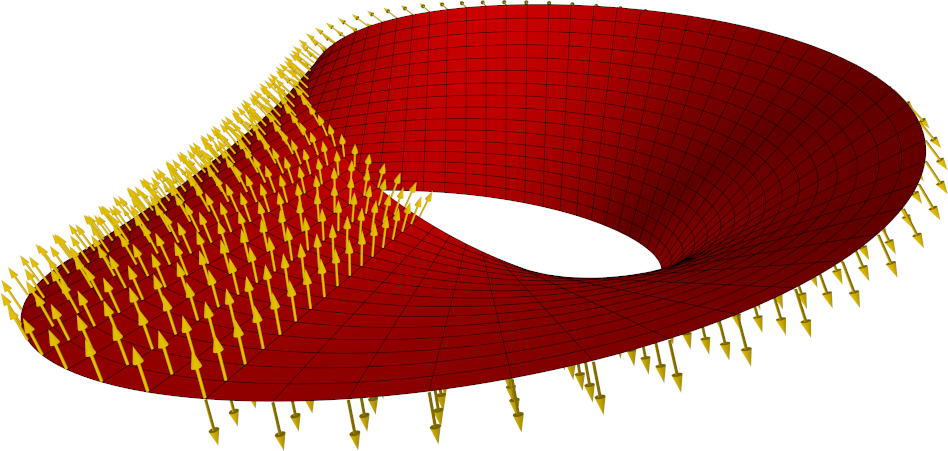
While already the initial announcement of Algosim 3.1 showed how to plot a surface in the form of a function graph, this example illustrates plotting a parameterised surface (as well as a vector field on a surface).
First, we need a parameterisation of the Möbius strip; we call this F. Also, for bonus points, we introduce a mapping NF that takes a surface parameterisation function, like our F, and returns its normal vector field. Using this mapping, the normal vector field of the Möbius strip is simply N ≔ NF(F). (This is a great example of the beauty of having functions as first-class objects.)
Here is the full code implementing this:
NF ≔ F ↦ ((u, v) ↦ normalized(diff(F(u, v), u, u) × diff(F(u, v), v, v)));
S ≔ ClearScene("Möbius strip");
AdjustVisual(S.axes, "visible": false);
AdjustVisual(S.view, "rθφ": ❨2.792, 72°, 20°❩);
F ≔ (u, v) ↦ ❨(1 + .5⋅v⋅cos(u/2))⋅cos(u), (1 + .5⋅v⋅cos(u/2))⋅sin(u), .5⋅v⋅sin(u/2)❩;
M ≔ surf([0, 2⋅π] × [−1, 1] @ F);
AdjustVisual(M,
"show parameter curves": true,
"parameter curve counts": ❨64, 16❩,
"line width": .75,
"unisided": true);
N ≔ NF(F);
VF ≔ VectorField([0, 2⋅π, π/32] × [−1, 1, 1/8] @ ((u, v) ↦ F(u, v) ~ N(u, v)));
AdjustVisual(VF,
"size": 0.1,
"anchor point": 1.03,
"color": "gold")
Yesterday, I published version 3.1 of Algosim.
The main new feature is a framework for 3D visualisation based on modern OpenGL and GLSL.
About 20 new functions make it easy to plot graphs, parameterised surfaces, parameterised space curves, vector fields, and 3D primitives and models.
In addition, several existing functions have been improved, as well as the language itself.
Det är svårt att inte bli tagen av nyheten om drottning Elizabeth II:s bortgång.
Hon var en av de offentliga personer jag hade allra störst respekt för. Hennes outtröttliga arbete under mer än sju årtionden präglades av orubblig integritet och värdighet ända till slutet: Hon tillsatte sin 15:e premiärminister så sent som i förrgår.
Samtidigt som jag känner sorg så finner jag tröst i det faktum att den 96-åriga drottningen knappast kunde ha slagit fler rekord eller lämnat ett finare arv efter sig. Det är inte många som fortfarande arbetar i den åldern. Det här är en saga som nästan inte kunde ha fått ett lyckligare slut.
Det är också med glädje jag ser hur värdigt BBC förmedlade nyheten om regentens bortgång.
Vad är det som gör något vackert? Vad är den själsliga upplevelsen av skönhet?
Den senare frågan tillhör medvetandefilosofin och är därmed utom räckhåll för vetenskapen, medan man beväpnad med kunskap om de världsliga biologiska, neurologiska och psykologiska fenomen som tangerar upplevelsen har en sportslig chans att kunna besvara den förra, betydligt torrare frågan.
Det förefaller uppenbart att skönhet är något subjektivt, åtminstone på någon nivå. Tänk bara på begreppet musiksmak. Samtidigt finns gott om utrymme för begreppsförvirring: Menar vi alltid precis samma sak när vi talar om skönhet? Finns det olika sorters skönhet? Och upplever två personer ett visst stimulus på samma sätt? (Josefin och Johan är, som bekant, överens om att himlen är ”blå” och gräset ”grönt”.)
Det kan vid en första anblick förefalla som att skönhet alltid primärt handlar om hur något uppfattas med ett visst kroppsligt sinne. Vacker musik handlar ju om ljudet, medan vacker natur eller arkitektur handlar om synintrycket. Men skönhet är ofta (om inte alltid) mer komplext än så; skönheten kan samtidigt involvera flera sinnen, känslor, tankar och tidigare erfarenheter.
För mig är (högskole)matematik något vackert, liksom minutiöst refaktoriserad programkod, en välformulerad text som med språklig korrekthet och precision förmedlar författarens tanke, omsorgsfullt utarbetad typografi och en textöversättning som vittnar om översättarens kompetens och noggrannhet.
Jag ser också skönheten i det kollektiva kunnandet.
Det finns absolut något vackert i hur två läkare oberoende av varandra gör samma bedömning eller sätter in samma åtgärder, allt enligt best practices. I hur två piloter hanterar en viss situation på samma sätt. I hur två erfarna servitörer dukar ett bord likadant.
Likaså är det nästan magiskt hur individuella artister var för sig men alla med samma musikaliska och känslomässiga korrekthet gestaltar Erik eller Christine i Fantomen på operan, som vore de extremiteter hos en och samma varelse.
Här kommer vi in på begreppet yrkesstolthet. Kanske handlar det om människans önskan om att vara en del av något större och mer meningsfullt.
Somliga företeelser är så vackra att deras skönhet bländar allt annat och får majoriteten av de ovan nämnda exemplen att framstå som triviala, ja rent av oväsentliga. Liksom sirenernas sång kan dessa helt förslava den drabbade.
Skönheten är, precis som livet självt, ett mysterium.
Den finns där, inom räckhåll men samtidigt bortom vad som kan begripas; den kan förnimmas men inte förklaras.
Virusrädsla drar mycket energi.
Hela tiden håller min hjärna koll på var det finns människor. Jag vet precis var alla är, när de kommer och går. Minsta avvikelse i normalt beteende uppfattas och analyseras, för kanske beror avvikelsen på en smittsam infektionssjukdom. Naturligtvis känner jag i detalj igen alla bekantas ”baseline” beträffande ljud från luftvägarna.
Jag vet alltid vilka kvadratcentimetrar hos min kaffemugg som varit i kontakt med något orent föremål. Vanligtvis är mitt korttidsminne inget vidare, men på den här fronten har jag alltid full koll. Även rummens volym och ventilation begrundas. Jag vill ju helst inte vara med en annan person i ett litet och dåligt ventilerat rum mer än högst tillfälligt. Givetvis anpassar jag kontinuerligt min andning efter aktuell risknivå hos luften.
Allt det här kräver mental energi – ja, rent av fysikalisk energi.
Extra jobbigt kan det bli i möten. Oavsett om det är ett arbetsmöte eller ett privat möte så är det viktigt för mig att hålla en hög professionell nivå, göra ett tryggt och förtroendeingivande intryck, komma med förslag och analyser av högsta möjliga kvalitet. Detta medför att jag utöver virusanalyserandet och det normala mötesdeltagandet också måste lägga energi på att dölja min rädsla, så att ingen lägger märke till den.
Ofta vill jag begränsa mötets längd för att minska risken för smittspridning, men detta helt utan att det går ut över mötets kvalitet eller resultat och utan att någon märker något eller upplever mig som oengagerad eller hård. Då går hjärnan på högvarv för att hitta lösningar som uppfyller dessa delvis motstridiga mål.
För några år sedan, före covid-19 och sjukskrivningen, hände det regelbundet att jag lyckades sitta blickstilla under ett helt möte, förstenad av rädsla och mentalt upptagen av alla analyser. Efteråt kunde jag knappt gå eftersom jag tillfälligt men fullständigt förlorat rörelseförmågan i ena benet och foten. (Det var ungefär samtidigt som jag hade problem med höften, så jag brukade maskera problemet genom att skylla på höften.)
Faktiskt kan jag drabbas av plötslig virusrädsla även när jag är fysiskt ensam, t.ex. om jag använder rösten och märker att den inte är exakt 100 % vad gäller kvalitet och styrka. Då kommer en betydande del av tankeverksamheten de kommande minuterna att behandla denna avvikelse.
Virusrädsla kan alltså vara väldigt utmattande för den drabbade – utan att detta syns på henne.
Det är därför den virusrädde aldrig får någon guldmedalj när hon i timmar framgångsrikt kämpat mot sin rädsla, men riskerar att straffas om hon någon gång misstolkas som oengagerad, lat eller arrogant, när hon egentligen bara är helt överbelastad i hjärnan.
Den här sortens rädsla manifesterar sig sålunda som en osynlig funktionsnedsättning, och sådana är, just på grund av deras osynlighet, knepiga.
Fortfarande.
Tyvärr.
(Men för egen del undviker jag att klaga på tillvaron. Trots virusrädslan mår jag bättre än vad jag gjort på över tjugo år.)
Sedan våren 2020 har jag varit vid god hälsa.
Visst har jag mina krämpor: Halsen gör sig påmind i tid och otid. Nästan ingen vecka är helt fri från den där lågmält panikartade oron som kommer på köpet med minsta aning om en begynnande luftvägsinfektion eller en rumsligt närbelägen smittkälla. Och fortfarande händer det att jag under mina promenader till och från jobbet stöter på en representant från den där gruppen människor som är lite bättre, lite finare och ganska mycket mer värda. De slagen i magen är hårdare men går också fortare över.
Dessa besvär har emellertid ingen stor inverkan på min vardag. Nästan varje dag är till syvende och sist en bra dag. Jag mår bättre än jag gjort på över ett kvarts sekel.
Jag kan inte själv ta på mig äran för denna lyckliga omständighet, som ju främst torde bero på sjukskrivningen och den selektiva serotoninåterupptagshämmaren.
I början av sjukskrivningsperioden kände jag en stor oro över vad som skulle hända när den tog slut. Jag trodde inte det var juridiskt möjligt med mer än några veckors sjukskrivning. Men sedan dess har den förlängts gång på gång och den är nu inne på sitt tredje år.
Dess förgänglighet oroar mig inte längre. Det beror inte på att jag börjat ta den för given, utan på att jag lärt mig att leva i nuet.
Jag vet förstås att den en dag kommer att ta slut. Här räcker det med en ny läkare som gått en annan skola, en ny bedömning från Försäkringskassan, en ny politisk majoritet.
Men egentligen förändrar dessa osäkerheter ingenting i grunden. Alldeles oavsett hur ens privatekonomi ser ut kan man drabbas av sjukdom, olyckor, krig och katastrofer. Det enda som inte tycks osäkert är varje levande varelses begränsade tid.
Det finns ingen naturlag som säger att varje människa skall leva hundra år i fred och harmoni, det finns ingen universell rättvisegaranti. Att universum inte fungerar så är smärtsamt övertydligt. (Därmed inte sagt att man som människa inte bör sträva efter dessa mål i allt som man företar sig.)
Snarare är det så att jag är exceptionellt privilegierad och lever under villkor som haren i parken, fågeln i trädet och också de allra flesta människor på jorden bara kan drömma om. Åtminstone gör jag det just nu.
Jag ser varje ny bra vecka som en bonus som jag försöker ta till vara på bästa sätt, inte minst genom att skapa. Sedan om hälsan håller i sig i en vecka till, i ytterligare ett år eller i ett halvsekel till, det är en fråga vars svar jag varken känner till eller efterfrågar.
Livet är som en ändlig vandring genom en oändlig herrgård – förunderligt och ibland skrämmande. Utan att veta vad som väntar härnäst går man från rum till rum och inreder dem med sina egna upplevelser, alltid inspirerad av det som tidigare generationer lämnat efter sig. Rummet som man för tillfället befinner sig i utgör just då hela ens värld, och det enda man kan göra är att inreda det så fint man bara kan.
Det är många virussjukdomar som sprids i samhället nu. Bland annat har vi en spridning av det nya coronaviruset som är mer omfattande än någonsin tidigare, i det närmaste explosionsartad.
Jag fick min andra vaccindos den 21 juli 2021 och enligt Region Östergötlands regler är jag därför inte berättigad till en tredje dos förrän den 21 januari 2022.
Det känns dock ofantligt dumt att vänta med denna spruta. Den tredje sprutan gör nämligen stor skillnad vad gäller skyddet, i synnerhet när det gått nästan ett halvår sedan den andra sprutan. Det är ju nu jag behöver skyddet – inte i sommar.
För egen del är det sålunda ingen poäng alls med att vänta, och även för samhället i stort torde reducerat dosintervall för fler vara av nytta. Det verkar nämligen som att det finns gott om obokade vaccinationstider i Östergötland. När jag tittade på schemat var nästan alla tider gröna.
Med tanke på min virusrädsla håller jag på att stressa till mig en hjärtinfarkt. Det känns inte roligt att vara dåligt vaccinerad när en sådan enorm smittvåg sköljer över landet.
Men nu i helgen upptäckte jag att Region Kalmar län bara kräver fem månaders intervall mellan dos 2 och dos 3, så i morgon åker jag (i egen bil) till Västervik för att få min tredje spruta.
Jag är dock arg på mig själv för att jag inte tidigare insåg att jag hade den möjligheten. Jag hade ju kunnat åka till Västervik redan i slutet av december. Jag är arg för att jag utsatt mig själv och personer i min omgivning för en fara som jag hade kunnat undvika.
Jag hoppas innerligt att jag inte är för sent ute, att jag inte blivit smittad av något de senaste dagarna och att jag inte kommer att bli smittad av något innan tredje dosen nått full effekt. Trots extremt strikta hygienrutiner går man inte säker.
Men förhoppningsvis kan mina höga stressnivåer minska något om 10 dagar eller så.
En stor mängd fyrverkerier sköts upp av privatpersoner runt om Linköping i går – och ju mer jag tänker på det, desto konstigare finner jag det att detta fortfarande är tillåtet.
Det finns flera problem med fyrverkerier:
Fyrverkerier är farliga för dem som tänder på och för personer i den omedelbara omgivningen.
Varje år inträffar olyckor där människor får allvarliga (och otroligt otäcka) skador i ansikte och på händer. Man kan få men för livet. Jag har själv inte träffat någon sådan, men jag misstänker att en person som t.ex. sprängt sönder ena handen eller förlorat ett öga eller två i efterhand ångrar sig.
Fyrverkerier medför en risk för omgivningen. Projektiler kan träffa närliggande strukturer och utgör dessutom en brandfara.
Varje år sker missbruk med fyrverkerier, där fyrverkerier avsiktligt skjuts mot andra personer eller strukturer.
Fyrverkerier skrämmer många djur, såväl sällskapsdjur som andra former av husdjur och vilda djur.
Detta är antagligen det största problemet. Förutom att djuren blir kraftigt skrämda för stunden så kan de fly i panik och då råka ut för olyckor. Varje år skadas djur svårt, ibland så illa att de måste avlivas eller dör av sig själva. Många djurägare kan intyga att detta är ett stort problem varje nyår. Även den nedskräpning som kommer av fyrverkerier och andra typer av atmosfäriska nyårseffekter kan orsaka allvarlig skada på djur som försöker förtära rester.
Självfallet orsakar fyrverkerier också en tillfällig störning för boende i området samt utgör en källa till nedskräpning och miljöförorening.
Dessa punkter talar starkt emot att fyrverkerier skall vara tillåtna, i synnerhet punkten om djurens hälsa, som är mycket, mycket stark.
Vad finns det då för fördelar med fyrverkerier? Jo, en enda: De som tycker om fyrverkerier får en stunds förströelse en gång om året.
Väger fördelen upp nackdelarna?
Nej, naturligtvis inte. Att några personer får en stunds förströelse några minuter väger inte upp att ett antal djur stressas ihjäl, en och annan människa får men för livet och otaliga djur och djurägare får uppleva några timmars mardröm.
Jag skulle inte vara lika tvärsäker om det fanns något som tydde på att fyrverkerierna skulle fylla ett mycket stort känslomässigt behov hos förespråkarna, så att ett förbud skulle orsaka omfattande och livslångt lidande för dessa. Men så tror jag inte att det är.
Jag skulle heller inte vara lika tvärsäker om det fanns något sätt att avfyra fyrverkerier utan att någon utomstående (djur eller människa) far illa. Men i Sverige är detta nästan inte möjligt någonstans. Det skulle i så fall vara mitt ute på fjällen i norr eller ute till havs.
Som jämförelse kan jag säga att jag inte är nämnvärt positivt inställd till ett förbud mot alkohol. Dels är det ju så att alkohol kan konsumeras helt utan att någon annan far illa, dels är det så att alkoholhaltiga produkter kan utgöra en sund och väldigt viktig del av en människas vardag.
I fallet med fyrverkerierna, däremot, är betydande men hos andra nästan oundvikligt och en stunds trivial förströelse för egen del kan aldrig rättfärdiga det.
 Häromåret noterade jag likheterna mellan mig och Locke.
Häromåret noterade jag likheterna mellan mig och Locke.
Ännu större är likheterna mellan mig och hunden Sally. Vi är nämligen båda däggdjur (klassen Mammalia) och har därmed snarlik fysiologi och stora likheter vad gäller psykologi och beteende.
Det finns förstås även olikheter, t.ex. vad gäller kognitiv förmåga, något som människor är duktiga på att framhålla.
Visst, jag kan på molekylär nivå redogöra för mekanismerna för aktionspotentialer och skelettmuskelkontraktion, och den statistiska fysik som ligger bakom dessa processer. Jag kan härleda Keplers lagar från Newtons lagar och gravitationslagen. Jag kan bestämma en algoritms tidskomplexitet.
Jag tror inte att Sally funderar på sådana saker, men å andra sidan är det inget vi brukar prata om, så kanske vet hon mer än jag tror!
I vilket fall som helst är dessa mina kunskaper och färdigheter egentligen ganska ytliga. Om universums och livets stora gåtor kan jag inte säga något alls: Varför är rummet tredimensionellt? Har universum alltid funnits? Vad är universum? Vad är själen (medvetandet)?
Och så vitt jag känner till kan inte heller Sally uttala sig om dessa frågor.
På det stora hela tycker jag därför att Sally och jag sitter i samma båt och att vi är ungefär lika kloka och kunniga.
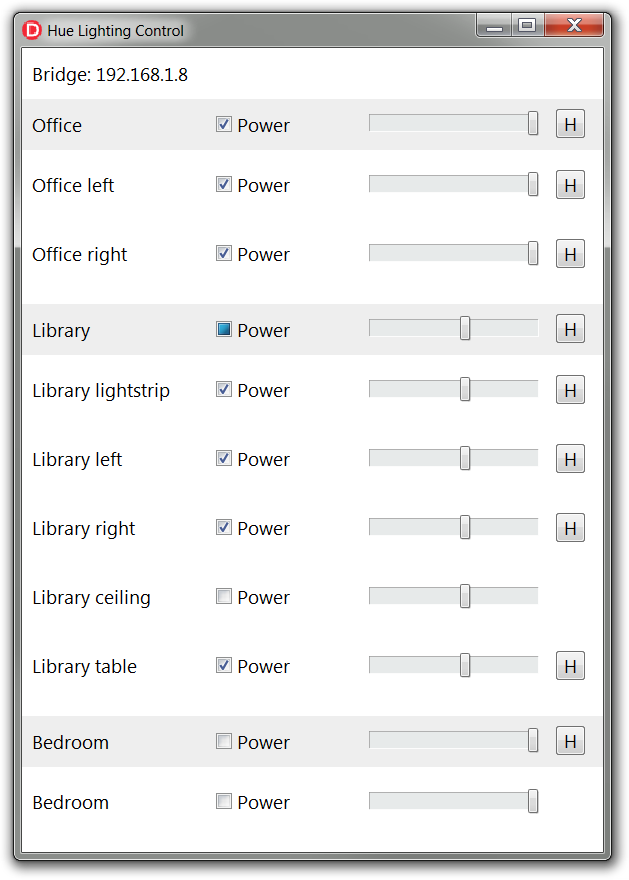 I recently upgraded most of the lighting in my flat to a Philips Hue system.
I recently upgraded most of the lighting in my flat to a Philips Hue system.
Actually, I had considered doing this for quite some time, but I had also been reluctant because of the Philips Hue set up process: The official way to set up a Hue system is by means of the official smartphone app, and I don’t own a smartphone. And even though I do have an Android tablet, its operating system version is no longer supported by the app.
I’m not impressed by these system requirements. First, my tablet is merely six years old, and so I consider it “new”. It is much newer than my twelve-year-old main computer. By not supporting “old” hardware, Philips is effectively encouraging people to throw away old hardware that is still working. That’s bad for the environment and the consumer’s personal finances.
Second, I’m disappointed that a computer-controlled lighting system cannot be controlled by a “real” computer (that is, a Win32 server or desktop computer), but has to be controlled by “toys” (smartphones).
I might understand that Philips doesn’t want to build a native Win32 desktop application, but IMHO, they should have built a web interface. Indeed, the Hue bridge is connected to the local network and has a web server. By navigating to the bridge’s IP, you are met with … the applicable open source licenses.
Here, they could have offered a web app for setting up, configuring, and controlling the lighting system. Such a web app would be accessible from any device on the network: desktop computers (Windows, macOS, Linux), laptops, tablets, smartphones, etc.
Eventually, I purchased a Hue system together with a new Android tablet, the cheapest I could find, which I used to set up the Hue system. Of course, now that the system is set up, it is mainly controlled using Hue dimmers and schedules. If I need to do something fancy, I can use the new tablet.
But I still was disappointed I couldn’t control the system from my main computer, so I ended up creating my own Win32 software for this purpose (see screenshot).
I somras publicerade jag en ny film som tar upp ämnet sexköp för funktionsnedsatta:
Filmen kan också ses på YouTube. Glöm inte att dela filmen.
Materialet finns även tillgängligt i textform med vissa fördjupningar. Dessutom har jag publicerat en sida med förtydligande frågor och svar.
I have published a video showcasing Algosim:
The video can also be watched on YouTube.
Både jag och kaninen Fernando är mycket glada över att det nu äntligen är sommar. Här är en bild på oss två:
I have published a few Delphi VCL units that make it easier to create high-quality Win32 desktop GUIs. Specifically, I have published code for a fluent task dialog API, a table dialog box, and a component that implements smooth animated resizing of forms.
Kanske lägger jag för mycket pengar på sprit?

 I have published the first version of my new mathematical software Algosim 3.
I have published the first version of my new mathematical software Algosim 3.
With more than 800 functions and 70 operators, including more than 320 mathematical functions, Algosim is a general-purpose mathematical software application and scripting language that lets you perform computations on numbers, vectors, matrices, images, sounds, and more.
While Algosim’s syntax is designed to closely mimic the notation used in ordinary mathematics to make it easy to learn and aesthetically pleasing, with functions as first-class objects and a comprehensive set of list-manipulation functions, it is also a fairly powerful language for list-based computations.
Algosim supports many aspects of 2D visualisation and can additionally visualise data as pixmap images, sounds, and MIDI music.
More than 40 000 automatic tests (close to 500 000 after parameterisation) are used to assert the correctness of the software and with a manual in almost 1000 pages, it should be relatively easy to get to know the application.
I have created a web site for the application, algosim.org, and published the complete source code there.
Spridningen av det nya coronaviruset är hög i Sverige och vaccinationen går framåt lika långsamt som en snigel i både motvind och uppförsbacke.
Det verkar som om även unga och friska personer kan bli ganska svårt sjuka – och även om man inte blir svårt sjuk riskerar man mycket långvariga besvär efter infektion. Dessvärre förefaller s.k. långtidscovid vara vanligt.
För att skydda mig själv och andra undviker jag nästan all onödig kontakt med andra människor. Förutom att jag går till jobbet – till fots, och jag tar omvägar för att slippa passera folk – så lämnar jag aldrig lägenheten annat än för matinköp en gång per vecka.
I höstas började jag lägga denna veckohandling på Maxi klockan halv tio på kvällen, strax före stängning, i hopp om att slippa trängsel, men i mina ögon var det alltid ”fullt” med folk där även den tiden. Varje vecka höll jag på att stressa till mig en hjärtinfarkt när jag sprang runt och försökte undvika alla tvåbenta virusfabriker. Därför har jag sedan ett par månader tillbaka valt att veckohandla samma tid men på en mer avsides affär.
Vid ett tillfälle var jag helt ensam som kund i den ändå relativt stora butiken, och det var otroligt skönt. Oftast är det dock ett par eller en handfull kunder där, men det brukar gå att hålla bra avstånd. (”Bra avstånd” betyder i min värld ungefär 10 meter.) Vanligtvis möter jag ingen kö alls i den enda öppna kassan.
I ett försök att minska min virusrädsla och kanske också lindra halsproblemen har jag ökat dosen SSRI. Detta betyder emellertid inte att jag har för avsikt att dra ner på den sociala distanseringen inom någon snar framtid, utan det är en ren oro- och ångestlindrande åtgärd.
Den gångna vintern var för övrigt den bästa någonsin för min del, dels tack vare det förbättrade hälsotillståndet, dels tack vare virusfriheten. Calicivirus och luftvägsvirus förekom nästan inte alls i samhället. Jag hoppas att svenskarna kommer att komma ihåg det nya hygientänket även under framtida vintrar så att dessa blir lika virusfria, men på den punkten är jag inte särskilt optimistisk. Alls. Jag är redan orolig inför nästa vinter.
Men den är långt borta. Så långt in i framtiden planerar jag inte.
Nu är i stället våren här och jag ser fram emot en varm och virusfri sommar (helst inte i respirator).
Det har nu gått över två år sedan halsproblemen så plötsligt uppstod i januari 2019.
Lyckligtvis har problemen blivit mindre uttalade med tiden, kanske tack vare ett allmänt bättre hälsotillstånd. Numera känner jag ganska ofta ingenting alls från halsen. Ibland kan det rent av gå en hel dag utan problem, i synnerhet om jag har fullt upp med spännande saker att göra på jobbet och hemma.
Däremot går det aldrig en hel vecka utan känningar. De flesta dagar drabbas jag av åtminstone en halsattack, när jag tycker mig förnimma något onormalt. Jag tänker då att en luftvägsinfektion är på gång och att jag kommer vara sjuk i flera veckor, orsaka besvär för arbetsgivaren och kanske få leva med residualeffekter som hosta och heshet i månader. Jag blir väldigt nervös. Men varje gång så försvinner ”problemen” av sig själva inom några minuter eller någon timme, bara jag börjar tänka på något annat.
Man kan tycka att jag borde ha lärt mig vid det här laget att det går över, att det inte är något farligt. Men inte. Varje gång känns det lite annorlunda. Ibland känns det konstigt i munhålan, ibland i svalget. Ibland ihållande, ibland bara vid provokation som t.ex. sväljning.
Jag antar att jag behöver lära mig att slappna av. Dessvärre vet jag inte hur. Att inte ha något att göra är som bekant inte en lösning. Antagligen är det åren av konstant hyperhög stressnivå före, under och efter läkarprogrammet som satt sina spår, och dessa spår är det inte lätt att bli av med.
Det verkar dock som om jag är på rätt väg. Trots halsproblemen mår jag bättre än vad jag gjort på över 20 år. Vid sidan av halsen besväras jag av mer eller mindre dagliga minnesbilder av det som hände på och efter läkarprogrammet, bilder som ger mycket stress och starkt obehag. Numera brukar de emellertid försvinna inom bara några minuter – återigen: när jag får annat att tänka på.
En av de största friskfaktorerna är att jag arbetar 50 %. Jag har snart gjort det i ett år med ersättning från Försäkringskassan, och det kan bli svårt att få ytterligare sådan ersättning beviljad. Det är lite tråkigt. Att förlora nästan halva sin inkomst är inte jättekul.
En bra dag har jag skapat en massa saker.
Det kan uppfattas som en helt okej sysselsättning: jag mår bra av att göra det, jag mår bra efteråt och skapelserna kan skänka ytterligare glädje i framtiden, ofta också åt andra. Ur ett utilitaristiskt perspektiv – vilket förstås är det perspektiv man alltid skall ha – är dessa förehavanden sålunda tillrådliga.
Emellertid hjälper inte denna intellektuella insikt mot förgänglighetssorgen: sorgen över att allt jag skapar oundvikligen en dag kommer att försvinna. Den problematiken har jag brottats med sedan högstadiet. Här behövs en copingstrategi.
Jag ser världen som en oändligt stor herrgård. Varje tid är ett eget rum, och under en människas liv går man sakta genom slottet från ett rum till nästa. I vart och ett av rummen ägnar man sig åt att göra det vackrare: man förskönar det med utsökta tapeter och magnifika gobelänger, praktfulla mattor och möbler, fascinerande saker och ting.
Inte förrän ett rum är fulländat går man vidare till nästa, med vetskapen om att det lämnade rummet alltid kommer att finnas kvar, även om ingen mer kommer att gå in i det. Och vad människorna beträffar kommer det alltid att finnas nya rum att inreda med en passion som aldrig tar slut.
Hur ser en riktigt bra dag i mitt liv ut?
En riktigt bra dag har jag skapat ett antal ordboksartiklar, skrivit ett svar eller två på Stack Overflow (i båda fallen med fokus på kvalitet), gjort ett fotografiskt eller matematiskt verk, utvecklat en mjukvara, skrivit en viktig text och ätit en massa kakor.
Bortsett från kakorna så är det gemensamma temat skapande. Jag tycker om känslan av att under dagen ha gjort världen lite vackrare, lite bättre, höjt medelkvalitetsnivån på Internet något. Och som så många andra människor, antar jag, att jag hyser en önskan om att lämna något efter mig, att göra ett avtryck (om än bara ett litet sådant).
Jag vet inte hur många gånger jag bevittnat en konflikt mellan två människor som är djupt osams.
Varje part är orubbligt övertygad om att hon i all väsentlighet är felfri själv och betraktar motpartens brister som fullkomligt uppenbara.
Nästan alltid förstår jag båda parterna.
I en del fall inser jag att jag själv skulle känna precis likadant som någon av dem om jag var i hennes sits. Ibland gäller detta båda parter samtidigt. Oftast finns det enskilda sakfrågor i respektive parts argumentation som är logiskt sunda och mycket lätta att förstå. Nästan alltid kan jag förstå hur respektive part känner sig eller åtminstone ana de psykologiska mekanismer som ligger bakom känslorna och agerandena.
Det jobbiga är att X inte ser det som jag ser hos Y, och vice versa.
Vad kan man göra i en sådan situation?
En tröst i sammanhanget, som jag insett de senaste åren, är att det i många fall inte är så fasligt viktigt att man gör någonting över huvud taget. För i många fall har respektive part ett betydande eget socialt och känslomässigt skyddsnät av människor och andra ting runt henne, som ger henne trygghet, stabilitet och glädje. Hennes konflikt med motparten är inte en stor del av hennes liv, den rubbar inte hennes balans, den får inga stora konsekvenser.
Men ibland är ena parten (eller rent av båda) extra utsatt(a), och man riktigt märker hur konflikten trasar sönder henne.
Vad kan man då göra?
Jag har inget mirakelsvar som alltid fungerar.
Men det förefaller rimligt att bekräfta varje part för sig, undvika att reta upp någon av parterna, och varje gång tillfälle ges (försiktigt och diskret) försöka så ett frö till förståelse för den andra partens situation.
Ofta känns det som om det enda jag gör på dagarna är att begå misstag.
Jag säger fel, glömmer bort ord, snubblar på orden, skriver fel, tänker fel, välter omkull kaffekoppen, glömmer saker.
Ibland har jag god lust att efter ett begånget misstag skriva en utförlig avvikelserapport med speciellt fokus på hur incidenten kunde inträffa och hur jag kan se till så att något liknande inte inträffar igen. Dock brukar jag sällan agera på dessa instinkter. Däremot brukar jag grubbla en hel del över misstagen och försöka ändra mig så att de inte upprepas. Sedan går det en dag eller två.
Att begå misstag är mänskligt.
Jag har ställt in tangentbordets bakgrundsbelysning så att den matchar skrivbordslampan!
Halsproblemen har blivit mer påtagliga den senaste månaden.
Vissa dagar upplever jag en uttalad obehagskänsla med lätt till måttlig smärta i munhåla eller svalg. Vid senaste anfallet häromveckan valde jag att ta en terapeutisk triad (paracetamol + ibuprofen + oxazepam), vilket kan uppfattas som en aningen aggressiv behandling, men med tanke på att mina typiska årliga förbrukningar av dessa preparat går att räkna med ena handens fingrar föreligger ingen nämnvärd missbruksrisk.
Hade det rört sig om en vanlig virusfaryngit hade smärtan kommit tillbaka inom åtta timmar, men som väntat kom den inte tillbaka alls. Senaste veckan har jag nästan inte känt av halsen över huvud taget, kanske för att jag har haft mycket att göra.
De dagar halsen gör sig påmind känns det som om det kommer att bli en lång och svår vinter. Det gäller, som vanligt, att jag håller mig fullt sysselsatt och undviker att tänka på LiU och virus.
Vad gäller virus är det också viktigt att hålla sig fysiskt borta från dem, i synnerhet med tanke på den återigen kraftiga smittspridningen av det nya coronaviruset. Det som är bäst för min OCD och PTSD sammanfaller med det som är bäst för samhället.
Förutom mina vanliga hygienrutiner har jag börjat att undvika alla typer av folksamlingar. Bortsett från att jag går till jobbet så lämnar jag bara lägenheten för att handla livsmedel två gånger i veckan, och det gör jag strax före stängning klockan tio på kvällen, i hopp om att möta en mycket glest befolkad butik.
Tyvärr är det sällan jag tycker det är tomt nog, ens då, och tyvärr är folk dåliga på att hålla avstånd. Om det är kö i kassan ställer jag mig tre meter bakom framförvarande kund och hoppas att en eventuell kund bakom mig ser hur jag tänker och också håller tre meter till mig. Men inte. Vanligtvis ställer de sig blott en meter bakom mig och andas och pratar med varandra.
Mer allmänt blir jag ledsen när jag i media ser rapporter om trängsel i köpcentra (att nöjesshoppa är knappast ”nödvändigt”), i kollektivtrafik, på fester. Eller när intervjuade shoppare skojar bort riskerna.
Vi har redan sett över 6 000 dödsfall i Sverige, många fler som blivit svårt sjuka, överbelastade sjukvårdsarbetare och allt fler rapporter om långtids-covid-19. Det senare syndromet (eller syndromen) verkar vara förhållandevis vanligt och verkar drabba även unga och friska – och det medför väldigt mycket lidande under väldigt lång tid (hur lång tid är det ingen som vet).
För egen del har tanken slagit mig att jag skulle kunna flytta till en avlägsen plats på norra Grönland.
Med flera mil till närmsta granne skulle även jag tycka att avståndet var tillräckligt. Skämt åsido vore det otroligt skönt att helt slippa rädslan för virus, att veta att det helt enkelt inte finns några virus som kan infektera mig. Det är också ljust och fint på sommaren.
Men jag antar att nackdelarna överväger. Till exempel kan jag ge mig sjutton på att det första som skulle inträffa efter att jag packat upp mina saker i en stor, fin stuga långt bortom all civilisation, är att jag drabbas av njursten.
Det mörka halvåret har nu gjort entré.
Vintern har varit en extra svår tid för mig de senaste åren, med stora konsekvenser för min hälsa.
I år har jag dock lite bättre förutsättningar för att klara av vintern. Av de fem friskfaktorer som har förelegat sedan i våras finns ju fyra kvar: det är ”bara” sommaren som är borta, med sin relativa virusfrihet, sitt ljus, sin värme och sin grönska. Jag har emellertid ett ess i rockärmen: eftersom jag jobbar 9–13 kommer det att vara ljust både när jag går till jobbet och när jag går hem från det. Det tror jag kommer att utgöra en viktig omständighet som kompenserar för det annars så skadliga mörkret.
Så förhoppningsvis kommer vintern 2020/21 att bli den första sedan läkarprogrammet som inte kommer att innebära blåljusfordon och sjukhusinläggningar.
Det gäller att jag förmår hålla uppe den fart jag fått under våren och sommaren, för när farten blir för låg så faller jag ihop. Vintern utgör en konstant bromsande kraft, så är farten för låg i början, bromsen för kraftig eller vintern för lång, så håller det inte.
Jag har redan märkt hur jag påverkas av mörkret och de ”höstförkylningar” som det pratas om i media.
Flera dagar har jag drabbats av förnimmelser från mun och svalg, vilket i sin tur orsakat kraftig oro. Jag tänker att en övre luftvägsinfektion är på gång: utanför fönstret är det ju precis så kolsvart som det brukar vara när sådana symtom uppträder. Jag tänker att jag kommer vara sjuk i ett par veckor, ha röstpåverkan och hosta i kanske en månad eller två eller tre. Jag är rädd för att jag kommer att sätta arbetsgivaren i klistret genom att inte kunna gå till kontoret, rädd för att jag inte skall kunna åka och träffa Canisarna på flera veckor. I min värld är en förkylning som jordens undergång. (Och nu har jag inte ens nämnt calicivirusen som jag är ännu mer rädd för.)
Men några timmar senare, när jag kommit igång med något spännande arbete, så försvinner plötsligt alla ”symtom”.
Det gäller att jag håller farten uppe.
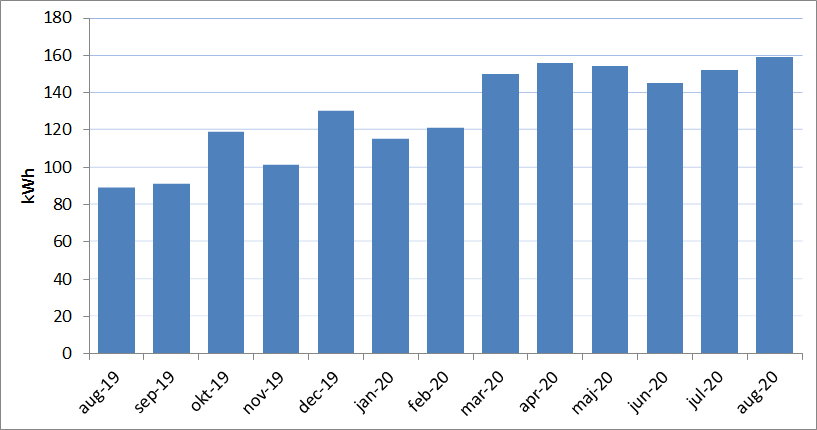
Det syns tydligt på min elförbrukning att jag ändrat livsstil under året. Till exempel är förbrukningen under augusti månad nästan dubbelt så stor som året innan.
Det är inte så konstigt eftersom jag flyttat ut från restaurangen och in i min egen lägenhet. Från att ha spenderat nästan all min vakna lediga tid på restaurangen så har jag inte varit där en enda gång sedan den 10 februari i år. I stället har jag spenderat all min vakna lediga tid hemma – och eftersom jag numera bara jobbar 50 % blir det ganska mycket. (Staplarna för oktober och december 2019 är antagligen höga p.g.a. sjukdom som gjorde att jag inte kunde gå till restaurangen.)
Utanför jobbet har jag sålunda gått från en tillvaro där jag aldrig var ensam till en tillvaro där jag alltid är ensam.
Jag känner mig mycket mindre ensam nu. Nej, jag publicerar inte tryckfel. Jag känner mig mindre ensam nu.
Det kan förstås delvis bero på ett allmänt förbättrat hälsotillstånd, men det finns nog också en specifik koppling till den nya sociala situationen.
Ja, jag älskade restaurangen och människorna som fanns där. De blev som en familj för mig. Men samtidigt fanns hos mig alltid en viss känsla av att den gemenskap jag hade där endast var ett substitut för mer ”riktig” gemenskap – om än ett fantastiskt fint substitut.
Från början, d.v.s. för flera år sedan, var jag bara en ovanligt trogen stamgäst, men med tiden blev jag mer och mer som en av personalen, en i familjen, en av dem. På så sätt blev ”substitutet” bättre med åren: mindre substitut, mer äkta vara.
Men på en del punkter var förbättring inte möjlig. Utöver de fasta, seniora medarbetarna, fanns det alltid yngre förmågor i personalen. Några enstaka var under 18, men desto fler i tjugoårsåldern. Dessa var oftast i parrelationer, ofta i samborelationer. Det gjorde att jag nästan varje dag såg (spår av) den typen av relationer, som alltid varit och förmodligen alltid kommer att vara något helt otillgängligt för mig. När jag gick hem till mig sent på kvällen för att sova några timmar, gick de hem till sina respektive. Det här blev en konstant påminnelse om mitt utanförskap och om begränsningarna hos mitt substitut.
Vid några tillfällen pratade en tjugoårig servitris sex och samlevnad med en sjuttonårig servitris som ville ha råd om preventivmedel. Det gjorde extremt ont i mig, men det visade jag inte. Ingen hade kunnat märka någon reaktion hos mig. Jag är lite stolt över det. Den här typen av diskussioner var emellertid inte särskilt vanlig, som tur var.
De dagliga ständiga påminnelserna om mitt annorlundaskap var ett större problem. Och så i mitten av januari i år kom en ofantligt stor påminnelse att spelas upp rakt framför ögonen på mig i baren. I någon månad försökte jag hantera stressen genom att bara låta tiden passera. Det blev blåljusbilar, sjukhusinläggningar, allt sådant.
Den 10 februari gav jag upp. Och den här gången hade jag tur. Det är långt ifrån alltid som ett fullständigt sammanbrott leder till något gott, men just den här gången så gjorde det som bekant det.
(Sensmoralen i den här historien är att det inte är en människas nivå av ensamhet som skadar henne, utan avståndet mellan hennes faktiska och hennes önskade nivå av socialt umgänge. Kan man inte ändra på den faktiska nivån, så kan man ändå (i teorin) minska avståndet genom att ändra den önskade nivån.)
När jag storstädade lägenheten för ett par månader sedan hittade jag mina sångnoter.
Jag hade då inte sjungit på över ett halvår. Halsproblemen jag haft sedan januari 2019, den kraftiga rädslan för luftvägsinfektioner och den konstanta stressen över röstens kvalitet gjorde att jag lade sången åt sidan.
Men hälsan förbättrades under våren och sommaren och när jag hittade noterna kunde jag inte låta bli att pröva att sjunga några av dem.
Jag blev förvånad över hur bra det gick.
Eftersom jag hade två förbetalda sånglektioner kvar valde jag då att utnyttja dem under augusti och september. Och även de gick bra. Det har aldrig gått så här bra förut. Det låter mestadels väldigt bra.
Halsproblemen är inte särskilt uttalade i dag. Det finns dagar då jag inte upplever dem alls. Men jag märker att det börjar reta i halsen så fort jag blir aningen understimulerad/uttråkad eller när det finns stressorer omkring mig (virus, LiU-logotyper, etc.). Nu är vi också på väg mot höst och sedan (i värsta fall) även vinter. Det är något jag fasar inför.
För att klara av det gäller det att jag fortsätter hålla fast vid de friskfaktorer som jag känner till. Framför allt är det viktigt att jag håller mig fullt sysselsatt med stimulerande projekt, fortsätter att jobba 50 %, och fortsätter att äta mat som är bra för halsen, framför allt SSRI och kakor. För att underlätta det senare har jag uppdaterat min kakpolicy så att jag nu kan äta ett paket varje dag, även på vardagarna.
Jag hoppas också att den ökade medvetenheten i samhället om smittspridning håller i sig över vintern.
After almost 20 years of service I have finally decided to retire my old Microsoft Internet Keyboard Pro keyboard. A few weeks ago, I replaced it with a new one from Corsair.
The last few months prior to the upgrade, I observed that the keys required quite a lot more force than normal to go down, and unless I happened to hit the key at its very centre, it often refused to go down at all, making rapid typing a nightmare. Needless to say, this very much had started to get on my nerves, especially considering that I spend almost all of my free time at the computer.
I even realised that I was astounded and greatly pleased by the effortless typing I was able to do at work on the cheap (but functional) $10 keyboard I have there.
Being a tenacious keyboard user that rarely sees the point in using the (in comparison) highly inefficient plastic rodent on my desktop, I am rather fastidious when it comes to keyboards. I need a full-size classic layout, two Windows key, and a menu key; I often use the Insert, Home, End, Del, PgUp and PgDn keys, even Scroll Lock and Pause. I also wouldn’t want to live without dedicated media and volume keys. Ideally, I also want browser keys and power management keys. And, to make it even more difficult for me to find a suitable product, I don’t want the keyboard to look like a control panel from a bizarre alien spaceship (a design that supposedly attracts teenage gamers).
Eventually, I chose Corsair’s K55 RGB Keyboard. So far, I’m mostly happy with it. I like light-emitting things. Unfortunately, however, like so many other companies, Corsair has failed to produce a high-quality software utility to accompany their hardware. But I can live with it.
One thing that really bothered me though was that I lost the OSD volume indicator that was part of the Microsoft IntelliType software. I was unsure what to do about this, before I realised that I happen to be a Win32 developer myself. So I made my own volume indicator using the gauge control I made the other night.
That’s the thing you can see in the top-right corners of the screens in the photograph above.
It’s kind of pretty, if I say so myself.
(But the OSD volume indicator doesn’t even come close to the prettiness of Sally, the dog.)
Det här är Locke:

Locke är en lockespindel som jag delat min lägenhet med ett tag nu. Det kan vara värt att poängtera att Locke alltså inte är en spindel (ordningen Araneae) utan en lockespindel (ordningen Opiliones). Båda ordningarna tillhör däremot klassen spindeldjur (Arachnida) i stammen leddjur (Arthropoda) i djurriket (Animalia).
Jag själv tillhör också Animalia, så Locke och jag har väldigt mycket gemensamt. På en molekylär, genetisk, cellbiologisk och fysiologisk nivå är det mest kosmetiska skillnader mellan oss. Men även om man bara tittar på beteenden har jag alltid slagits över hur lika alla djur är. Jag har alltid sett mig själv i en hund, hare eller råtta – eller ett leddjur. Jag tror att de flesta människor kraftigt överskattar människans särställning inom Animalia. Kanske är det liknande mekanismer som ligger bakom idéer om överlägsenheten hos någon specifik människoras.
Locke brukar dyka upp någon gång i veckan för att sedan plötsligt försvinna igen. När jag tog bilden ovan så hade han ställt sig och vilat mitt på hallgolvet, vilket jag personligen inte tycker är lämpligt ur säkerhetssynpunkt. Det händer nämligen att jag går i hallen utan att titta särskilt noga på golvet. Ibland går jag i hallen när det är mörkt och jag inte ser golvet. Det är alltså farligt för Locke att vistas där.
Därför valde jag att flytta honom till en säkrare plats i lägenheten.
Att flytta en lockespindel kräver inga redskap. Det är lätt att få upp en lockespindel på sin hand och sedan låta djuret vandra runt på händer och armar medan man går till lämplig avstigningsplats. Men givetvis måste man hela tiden vara mycket försiktig så att man inte oavsiktligt skadar djuret. Det går inte att flytta djuret på annat sätt än genom att låta det vandra över en yta eller flytta en yta som djuret står stabilt på.
Här är några fotografiskt sett bättre bilder av lockespindlar som jag tog för 10–20 år sedan:


Vägen jag går till och från jobbet är så vacker nu. Grönskan är nästan överväldigande.
När jag går här kan jag ta ett djupt andetag och låta mig uppfyllas av harmonin i naturen, lägga alla sorger och besvär åt sidan. Inget av det syns här.
 Nu sent på kvällen fick jag ett sådant där otäckt telefonsamtal igen. Den här gången är det en väldigt nära familjemedlem som kan vara mycket allvarligt sjuk. Det är vid sådana här tillfällen det är tufft att vara ensam. Jag sitter i min lägenhet, hade tänkt se på en film i kväll, men försöker nu dämpa ångesten med Sobril. (Det känns lite som om de högre makterna märkte att jag började må för bra.)
Nu sent på kvällen fick jag ett sådant där otäckt telefonsamtal igen. Den här gången är det en väldigt nära familjemedlem som kan vara mycket allvarligt sjuk. Det är vid sådana här tillfällen det är tufft att vara ensam. Jag sitter i min lägenhet, hade tänkt se på en film i kväll, men försöker nu dämpa ångesten med Sobril. (Det känns lite som om de högre makterna märkte att jag började må för bra.)
Uppdatering: Men med lite tur är det inte så illa som det lät i telefonen. Vi har i släkten förmodligen varenda gen som finns som predisponerar för mental ohälsa. Ni som läser min webbplats vet att jag är en extremt känslig/känslosam person, och det är jag inte ensam om i släkten. Så den information jag får via telefon är ibland kanske inte så otäck som den låter. (Dessutom börjar Sobrilen verka nu, känner jag. Som vanligt tog jag en ... ”inte jättelåg” dos.) Situationen i hela min familj har också försämrats rejält sedan det som hände på läkarprogrammet. Dels har förstås mina föräldrar varit oroliga när jag mer eller mindre varit suicidal i flera års tid, dels har det här traumat lett till andra, stora och mycket tråkiga, konsekvenser inom familjen. Jag önskar så att LiU bara hade låtit mig sluta. Kanske till och med sagt ”Gud, vilket liv du levt, men nu skall vi göra allt vi kan för att hjälpa dig. Men vore inte en paus bra just nu?”. De har gett mig och min familj men för årtionden. Jag kommer aldrig förstå varför deras agerande var nödvändigt.
Vi måste ta hand om varandra och vara snälla mot varandra. Vi är alla sårbara och långt ifrån perfekta människor. Men vi måste göra vad vi kan för att göra gott.
 Förra veckan berättade jag om mitt största problem som har att göra med att både äta kakan och ha den kvar.
Förra veckan berättade jag om mitt största problem som har att göra med att både äta kakan och ha den kvar.
Faktiskt har jag samma problem med kakor av mer konkret natur.
De flesta dagar som jag jobbar äter jag inga kakor alls, men på helgerna brukar jag se till att ha kakor hemma. Av både ekonomiska och hälsomässiga skäl har jag emellertid som kakpolicy att aldrig äta mer än två paket kakor om dagen.
Vanligtvis köper jag fyra paket på fredagskvällen, med planen att äta ett samma kväll, ha två till lördagen och ett till söndagen. Men under lördagen har jag ofta svårt att begränsa kakätandet. Det händer lätt att jag framåt eftermiddagen bara har fyra eller åtta kakor kvar av dagens ranson, samtidigt som jag känner mig väldigt kaksugen. Å ena sidan vill jag äta kakorna då, å andra sidan vill jag förstås inte vara utan kakor under lördagskvällen och söndagen.
Jag vill både äta kakorna och ha dem kvar.
För övrigt kan jag nämna att jag gått upp en del i vikt de senaste månaderna. Från att ha varit underviktig är jag nu åter normalviktig.
Efter en del krångel blev jag sjukskriven 50 % fram till mitten av juni. Därför arbetar jag bara fyra timmar per dag – och får pengar från Försäkringskassan vilket delvis kompenserar för inkomstförlusten.
Den nya arbetssituationen utgör förmodligen en stor del av förklaringen till mitt kraftigt förbättrade hälsotillstånd de senaste två månaderna. Jag har väldigt svårt för kontorsarbete, att sitta vid ett och samma skrivbord från tidig morgon till sen eftermiddag. Långsamheten orsakar en instängdhetskänsla och en hel del stress. Bland annat får jag alldeles för mycket tid till att grubbla över livets orättvisor och att stressa upp mig över tänkbara hälsoproblem i mun och svalg.
Men att jobba fyra timmar per dag fungerar otroligt bra. Numera kan jag till och med tycka att det är roligt att gå till jobbet. Och det är numera förhållandevis sällan som jag upplever den förhatliga obehagskänslan i svalget.
Sommarens intåg har även den påverkat hälsan positivt. Jag är otroligt känslig för miljön omkring mig, den påverkar mig jättemycket. Jag har mycket svårt för mörkret, kylan och – framför allt – luftvägs- och calicivirusen under vintern. Jag har inte utfört någon rigorös statistisk undersökning, men jag tror att det hos mig föreligger ett tydligt samband mellan vinter och exacerbationer vad gäller mental ohälsa.
Paradoxalt nog har den pågående covid-19-pandemin har också påverkat mig positivt. Som nämnt har jag utvecklat en svår rädsla för vinterns patogener de senaste åren. Men det nya hygientänket som föranletts av pandemin – där folk stannar hemma vid minsta sjukdomssymtom, håller avstånd till varandra, tänker på handhygienen o.s.v. – har gjort att spridningen av dessa virus under sena vintern och tidiga våren minskat. Det har lett till en reducerad stressnivå hos mig.
Det hela är egentligen högst osannolikt: Under vintern gick jag till sjukvården för att få hjälp med min virusrelaterade rädsla och OCD och fick läkemedel som skulle hjälpa mig att leva i en omvärld fylld av luftvägs- och calicivirus och människor som inte alltid tänker på smittvägar. Men direkt efteråt anpassas hela omvärlden i någon mening efter mig och min fobi. Sådant händer ju bara inte!
Det verkar för övrigt som om jag inte är ensam om att få min smittorelaterade ångest och OCD lindrad av covid-19. Jag läste i morse en artikel i brittiska BBC där samma fenomen omnämns.
(Samtidigt får man inte glömma att covid-19 är en dödlig sjukdom som bland annat kostat väldigt många människoliv och orsakat enorma ekonomiska skador. Eventuella mentala hälsovinster hos oss med OCD väger inte upp mot de tragedierna. Om jag var omnipotent hade jag naturligtvis utrotat det nya coronaviruset utan att tänka.)
Ytterligare en faktor som förbättrat min hälsa avsevärt är att jag numera är hemma och arbetar med en massa projekt, vilket håller mig sysselsatt och engagerad. Som bekant spenderade jag ju tills för några månader sedan all min lediga tid på restaurangen, i princip sysslolös. Det började med att jag var livrädd för att ha fått brev från Linköpings universitet eller domstolen och därför inte vågade gå hem från restaurangen på eftermiddagen. Sedan blev det en vana.
Så just nu mår jag bättre än vad jag gjort på länge, även om marginalerna inte är så stora: PTSD:n finns där hela tiden. Det går inte en dag utan att jag plågas av minnesbilder från tiden på och efter läkarprogrammet, från rättsprocessen. Jag tänker på allt som klasskamraterna och lärarna och rektorn och rättspsykiatrikern skrev och sade. Jag drömmer fortfarande mardrömmar om dem på nätterna. Jag inser att jag aldrig (igen) kommer att bli lärare, läkare eller pilot. Det gör otroligt ont att tänka på det, och det är en sorg jag förmodligen kommer att bära med mig resten av livet. Däremot kan jag just nu hantera de här tankarna. Jag kan mota bort dem genom att hålla mig sysselsatt med sådant som fängslar mig.
Men framtidens himmel ser oroväckande molnig ut: dels kommer det bli vinter igen (och den här gången kanske människor är nära varandra och sprider calicivirus hej vilt omkring sig), dels kommer min sjukskrivning eventuellt att upphöra om någon månad eller så. Då kommer jag få det mycket svårt att klara ekonomin, inte minst som CSN vill ha flera tusen kronor av mig med jämna mellanrum (för en utbildning som bara gett mig PTSD).
Jag vill alltså ha pengarna från en hundraprocentig anställning och arbetstiden hos en femtioprocentig sådan. Det är ett klassiskt fall av att både vilja äta kakan och ha den kvar.
Det här är mitt största kakproblem.
Med lite digital bildbehandling kan man göra om ett fotografi på en fjädermygga utanför fönstret till en bild av en insekt som står på vattenytan i en sjö:
Inte helt oväntat är jag mycket förtjust i det vackra försommarvädret. Ljus, värme och grönska mår jag bra av. Träden har blivit alldeles gröna av blad och vita av blommor. Jag hoppas det aldrig blir vinter igen.
Utanför lägenhetsfönstren vimlar det av fjädermyggor. De är fina djur. Jag kan inte fotografiskt återge dem med samma häpnadsväckande kvalitet som man ser i naturfototävlingar (t.ex. på BBC:s webbplats), bland annat eftersom jag inte har utrustning för det. Men helt dumt blir det ändå inte:
Tittar man noga på den andra bilden i förra artikeln ser man att jag fortfarande använder Windows 7.
Eftersom supporten för Windows 7 – som släpptes för snart elva år sedan – har upphört bör man inte längre använda operativsystemet på Internetuppkopplade datorer. (Anledningen är att inga nya säkerhetsuppdateringar nödvändigtvis kommer att skickas ut, så eventuella säkerhetshål som upptäcks kommer att förbli öppna.)
Även datorn i sig är ett drygt årtionde gammal, men den fungerar fortfarande lika bra som när den var ny. Jag har bara uppgraderat grafikkort, internminne och optisk enhet.
Jag har aldrig tyckt om slit och släng, och det gäller även datorer. När jag väl köper en ny dator, vilket jag inte gjort många gånger i livet, är jag inte snål, utan väljer komponenter i det övre prissegmentet. Jag spenderar trots allt större delen av min lediga tid vid datorn, och använder den till det mesta. Och kanske ännu mer relevant: när jag köper en dator, är tanken att jag skall kunna använda den under många år framöver – minst ett årtionde eller två.
Det är rent av något vackert med att använda något under en längre tid. Det blir roligare och roligare att använda föremålet ju mer historia det har.
Jag är dock osäker på hur pass bra Windows 10 skulle fungera på så här pass gammal hårdvara, så den påtvingade OS-uppgraderingen kan medföra ett likaledes påtvingat datorbyte.
Det känns inte roligt. Jag har ju egentligen inget behov av en ny dator. Datorbyte är dessutom inte enbart dåligt för plånboken, utan också för miljön. Det känns tråkigt att bli påtvingad ett sådant bara för att det finns människor som avsiktligt skriver och sprider illasinnad kod. Det är så onödigt.
En dag häromveckan när jag satt mig vid datorn för att skriva enhetstester inträffade en olycka. Jag hade just hällt upp en kopp kaffe som jag gjort från kaffepulver och 80-gradigt vatten från min fina vattenkokare. (Nescafé Lyx-glasburken var ny för dagen, och det är få saker som lukar så gott som pulvret i en alldeles nyöppnad sådan.) Men precis när jag lyft kaffekoppen från skrivbordet, samtidigt som tankarna var hos mjukvaruprojektet och därmed en bit bort från den fysiska omgivningen, gjorde korsdraget mellan balkongdörren och sovrumsfönstret att det senare smällde igen på ett högst ljudligt sätt. Jag ryckte till och fick flera centiliter kaffe över tangentbordet.
Som tur är använder jag ett Microsoft Internet Keyboard Pro från år 2000. Det är en kvalitetsprodukt från en svunnen tid då stora företag fortfarande producerade kvalitetshårdvara för PC utan att rikta in sig specifikt på spelsegmentet. I dag finns det också påkostad hårdvara, men designen brukar avskräcka alla utom 12-åriga pojkar med datorspel som största intresse.
Hur som: tack vare denna lyckliga omständighet var det bara att skruva isär tangentbordet och rengöra det i diskhon:
Efter rengöringen var det som nytt igen:
Jag kan tänka mig att många med smittorelaterad ångest och OCD lätt blir arga när människor i deras närhet genom oförsiktighet utsätter dem för smittorisk.
Det är väldig förståeligt. Föreställ dig en person som är livrädd för att bli smittad och som hela dagen lyckats hålla smittorisken på en mycket låg nivå tack vare strikta hygienrutiner och en ständig medvetenhet om smittfarorna i omgivningen (människor, fomiter, …). Sedan hostar en snuvig person på henne. Dels riskerar hon att bli sjuk, dels har alla hennes ansträngningar under dagen kanske varit förgäves. Om OCD:n är svår kan incidenten också leda till att resten av dagen går åt till att duscha, tvätta kläderna, raka av sig håret, … .
Ponera vidare att hon blir sjuk. Då får hon lida i en eller två veckor. Eller ännu längre: hostan kan sitta kvar en månad. Hon kan inte gå till jobbet och missar några gånger på sina fritidsaktiviteter. Allt det här leder till sekundära bekymmer. Och allt detta bara för att människan som hostade inte hade sunt hygienförnuft! Så onödigt.
Jag förstår att man tänker så, inte minst som jag själv lider av smittorelaterad ångest och OCD, om än i förhållandevis måttlig tappning.
Men jag är väldigt noga med att inte bli arg.
Jag påminner mig om att det viktigaste jobb varje människa har i livet, är att vara en så god medmänniska som bara möjligt till alla människor omkring henne. Så om jag blir arg och är tvär mot någon som oavsiktligt utsatt mig för en dos virus begår jag själv ett större fel än henne.
Eftersom min problematik är förhållandevis måttlig har jag inga problem med att hantera den potentiella irritationen, och jag har inte blivit märkbart arg på någon av den här anledningen på många år. Det är sällan jag ens blir arg inombords.
(Däremot har jag under senaste veckorna känt mig lite irriterad över hur närgångna en del kan vara i kassan i livsmedelsbutiken, trots att det i och utanför butiken finns mängder med affischer som påminner oss om att hålla avstånd till varandra.)
Även om min egen smittorelaterade ångest och OCD inte har förvärrats nämnvärt av den pågående coronaviruspandemin, så finns det förmodligen många människor med värre sådan problematik för vilka epidemin orsakar stor psykologisk och känslomässig skada. Det här ämnet har bland annat behandlats av BBC.
Något som kanske de flesta av oss med den här problematiken har gemensamt, däremot, är uppmärksamheten på hygienrutiner och på händelser i omgivningen, vilka är intressanta ur en smittosynpunkt. Jag noterar varje gång någon har händerna i ansiktet, hostar i handen eller vidrör vattenglaset där det senare kommer att komma i kontakt med läpparna. Det är ett väldigt invant beteende hos mig att reagera, om än bara för mig själv, på sådana händelser.
Det här är emellertid observationer som jag oftast är noga med att hålla för mig själv: jag påpekar nästan aldrig andra personers beteende när det gäller personliga hygienrutiner.
Det finns flera anledningar till det. En är att många förmodligen har väldigt svårt att t.ex. undvika att vidröra ansiktet med händerna – sådant sker reflexmässigt. Samtidigt tror jag att det finns en ganska utbredd uppfattning i samhället att sådant beteende inte ens är ”fel” eller nämnvärt farligt. Ett påpekande torde sålunda oftast resultera i ingenting, ibland i irritation.
Men den viktigaste anledningen är att jag tror att det kan vara direkt skadligt att påpeka. Det finns nog många känsliga människor som liksom mig själv är predisponerade till oro, ångest och OCD. Ett påpekande kan för en sådan person sätta igång en negativ process åt det sjukliga hållet. En person som inte tidigare alls tänkt på sådana här saker, men som är känsligt lagd, börjar tänka på dem. Det blir större och större.
Jag vet inte hur stor den risken är, men jag anar att den är nämnvärt nollskild.
Om man slarvar med de personliga hygienrutinerna kanske man blir förkyld eller magsjuk en eller två gånger extra om året. Men man får väga det mot att gå runt och vara konstant hyperstressad för smittor. Jag vet att min rädsla för förkylnings- och calicivirus under vintern orsakar väldigt mycket stress hos mig, och jag vet att det finns relativt många som har ännu värre problem än vad jag har.
(Däremot skall man naturligtvis följa myndigheternas råd under pågående epidemi, som kostar många människoliv och stora ekonomiska förluster. Det är nu det är viktigt för alla att tänka på hygien och smittorisk.)
Jag har alltid varit ”väl medveten” om vikten av goda personliga hygienrutiner för att minska risken att bli sjuk eller att själv sprida smitta till andra. Och de senaste åren har jag utvecklat en ganska kraftig fobi för vinterns smittor. Så jag är ”väl förberedd” för de hygienrutiner och beteenden som nu rekommenderas av myndigheter världen över i syfte att hantera covid-19.
Några av mina hygienrutiner i korthet:
Jag tvättar alltid händerna noggrant när jag kommer hem efter att ha varit ute. Det rekommenderas att man tvättar händerna åtminstone 20–30 sekunder, men jag tvättar i en minut. Jag är noga med att skrubba alla delar av händerna: handflatorna, handryggarna, mellan fingrarna, tummarna, fingertopparna, nagelbanden. Efter noggrann intvålning och skrubbning sker noggrann sköljning, också den med skrubbande.
När jag varit ute och handlat tvättar jag händerna två gånger: först direkt när jag kommer hem, och sedan en gång till efter att jag packat upp varorna (som kan ha virus på sig) och tagit av mig utekläderna (samma anledning), men innan jag tar på mig innekläderna.
Om jag, när jag är hemma, behöver ta i något föremål som jag använt ute, t.ex. mobiltelefon eller plånbok, så tvättar jag händerna direkt efteråt.
Om jag någon gång tvättar händerna på en offentlig toalett, och det föreligger påtaglig risk för smitta, brukar jag också se till att stänga av kranen med papper. Annars riskerar jag ju att kontaminera händerna det första jag gör efter handtvätten!
Jag har aldrig händerna i ansiktet utanför hemmet. Det här verkar vara något som är svårt för de flesta att låta bli, men jag fick redan som barn lära mig att man inte gör så, och det sitter i.
Det är också självklart för mig att inte ta i muggar, glas, porslin och bestick på en del av ytan som kommer att komma i kontakt med munnen. Kaffekoppar håller jag alltså på behörigt avstånd från den övre kanten.
Jag undviker att i onödan vidröra saker utanför hemmet, i synnerhet vanliga typer av fomiter.
Om jag behöver hosta eller nysa utanför hemmet så riktar jag mig mot golvet eller ett hörn av rummet och/eller gör det i armvecket. (Det är ur smittspridningssynpunkt en dålig idé att hosta eller nysa i handen.)
Jag håller avstånd till andra människor när jag är ute. Om jag tvingas passera någon på kort avstånd ser jag till att pausera andningen under mötet. Alternativt andas jag in före mötet och andas ut efter mötet, för att skydda den andra personen respektive mig själv. (Men så resonerar väl alla? För några år sedan kom jag förresten på ett namn för den här rutinen: ”mötesrespiration”.)
Jag har aldrig andra människor hemma i min lägenhet, så där föreligger nästan ingen risk för mig att bli smittad. Därför har jag mycket färre hygienregler i hemmet. Till exempel kan jag vidröra ansiktet.
Det här är alltså hygienrutiner som jag normalt sett har under vinterhalvåret – och i synnerhet under calicivirussäsongen – för att skydda mig mot övre luftvägsinfektioner och gastroenterit. Jag har sålunda knappt behövt ändra mina rutiner alls för att uppfylla myndigheternas rekommendationer.
Trots den fördelen är/var min virusfobi, som alltså inte har något med covid-19 att göra, ändå ett kliniskt problem eftersom den orsakar/orsakade väldigt höga stressnivåer och sekundära problem. Jag har därför påbörjat medicinering med SSRI.
Konstigt nog är min stressnivå inte negativt påverkad av covid-19. Det är snarare så att jag är mindre stressad nu än vad jag var för en eller ett par månader sedan.
Medicineringen kan vara en bidragande orsak, men jag tror den är ringa. Att jag bara jobbar 50 % har nog haft betydligt större inverkan: Jag mådde väldigt dåligt av att sitta på ett kontor åtta timmar per dag. Dessutom kan covid-19-situationen paradoxalt nog ha haft en stressreducerande effekt hos mig, av flera orsaker:
Numera stannar folk hemma även vid ringa förkylningssymptom. Det är ju en fullständig dröm för alla virusrädda!
Normen vad häller hygienrutiner i samhället har förskjutits åt mitt håll – jag har blivit mer ”normal”. Möjligtvis finns det psykologiska vinster med det.
Det råder numera en allmän känsla i samhället av att situationen inte är ”normal”, och det stämmer mer överens med hur jag själv känner mig. Jag har varit väldigt vilsen ända sedan jag slutade på MAI, och de personliga kriserna har avlöst varandra. I min värld har det varit en kaotisk undantagssituation i flera års tid. Nu känns det lite som om världen runtomkring mig är på samma våglängd.
Samtidigt får man inte glömma att covid-19 är en dödlig sjukdom, i synnerhet hos riskgrupperna, de äldre och sjuka. Många har dött och många fler kommer att dö. Ingen psykologisk vinst hos mig väger upp det. Varje dödsfall är en ofattbar tragedi för de som drabbas. Och oron hos dem som ännu inte drabbats är mycket förestålig: de allra flesta av oss tillhör en riskgrupp eller har någon närstående som gör det. Covid-19 är en tragedi för oss alla.
Jag fick ett telefonsamtal från min mor. Innehållet i samtalet är för hemskt och privat för att prata om, men det handlar om konsekvenser av det som hände på läkarprogrammet för tre år sedan. Jag har tagit fyrdubbel dos Sobril men känner mig fortfarande jättestressad och känner inte att jag har någon att vända mig till och prata med.
Jag önskar så att Helen, Stergios och Ann-Charlott och mina gamla klasskamrater inte hade gjort det som de gjorde. Det har lett till så enormt mycket lidande för så många personer.
Bakgrund: Ett upprivet sår, Sjukhus och Situationen.
Jag har en längre tid känt att det varit svårt att jobba åtta timmar per dag. Jag tror generellt sett att jag har lite svårt för kontorsarbete där det inte händer så mycket: jag känner mig lätt instängd och min hjärna får alldeles för mycket tid till att älta saker. Och jag har knappast haft ont om saker att älta de senaste åren. Jag har fått allt svårare att koncentrera mig på arbetet någon längre tid, och känt mig allt mer stressad över att sitta vid datamaskinen på jobbet åtta timmar i sträck varje dag.
Och den senaste tidens tråkiga händelser gjorde att bägaren rann över.
Jag fick en läkartid i måndags för att diskutera sjukskrivning, men en halvtimme före mötet kontaktade de mig och förklarade att vårdcentralen inte kunde hantera mitt sjukskrivningsärende. De menade att jag i stället skulle kontakta psykiatrin. Jag gjorde det, men de kunde inte behandla frågan förrän tidigast nästa vecka.
Därför kom jag och min chef i stället överens om att jag går ner till 50 % (utan någon form av sjukskrivning) från och med i måndags.
Det har fungerat bra. Jag har mått betydligt bättre. Men det är bara en tillfällig lösning, för det fungerar inte rent ekonomiskt för mig att arbeta 50 %. Jag kommer att gå minus några tusen kronor per månad, och om situationen inte ändras kommer alla mina pengar att vara slut inom halvtannat år.
Jag vet inte hur jag skall lösa det problemet.
Bakgrund: Ett upprivet sår och Sjukhus.
De senaste dagarna har kriserna utlöst varandra: en nattlig panikpromenad ut i skogen, en natt där jag försökte dämpa ångesten med sprit, två turer i blåljusfordon och tre sjukhusbesök.
De senaste åren har som bekant restaurangen och människorna där utgjort min trygghet, vilket till viss del kompenserat för att nästan ingenting annat fungerat i livet. Den utgjorde ett substitut – ofta ett fantastiskt bra sådant – för mer traditionella sociala relationer och fritidssysselsättningar och gav mig, utöver vänskap och mycket värme, en fast punkt i tillvaron, ett sammanhang och något att bry mig om. Restaurangen gjorde att jag oftast stod ut med tillvaron, om än med liten marginal. I synnerhet rättsprocessen mot LiU utgjorde en enorm källa till smärta och stress, men tack vare människorna på restaurangen klarade jag av det.
Nu när jag inte längre har restaurangen att gå till är det väldigt tomt. Jag är för ledsen, ångestfylld och stressad för att kunna koncentrera mig på något, så jag kan inte heller jobba. Det enda jag kan göra är att sitta hemma och försöka hantera sorgen, ångesten, hopplösheten.
Sjukvården har väldigt lite att erbjuda personer med min typ av problematik, eftersom problemen egentligen inte är av medicinsk natur. Jag vet det och läkarna vet det, så vi är överens.
Det som hade behövts var snarare ett mer tolerant och förstående samhälle. Det syns inte på mig, men när det kommer till saker som att ta sig fram på arbetsmarknaden eller att ta för sig och ta plats i sociala relationer, så är jag som en femåring i en manuellt växlad bil – jag klarar inte av det. Lägg till högkänslighet, stort behov av trygghet och fysisk närhet, stor etik-, plikt- och ansvarskänsla och du har receptet på en säker tragedi.
Jag älskade att undervisa i matematik på universitetet och presterade en bra bit över medel på t.ex. kursutvärderingar. LiU kunde ha varit lite flexibla och låtit mig fortsätta med det, trots att jag inte var disputerad. Jag menar, om samhället hittar en person som har alla odds emot sig men ändå lyckats hitta sin plats i livet, som verkligen fungerar perfekt för alla inblandade, varför inte låta personen fortsätta, även om det kräver lite flexibilitet?
Och efter den där hösten på läkarprogrammet kunde LiU ha låtit mig lämna programmet frivilligt. De hade inte behövt initiera den där treåriga rättsprocessen som gav mig PTSD och oöverkomliga juridiska problem. Jag hade redan lämnat dem innan de ens påbörjat processen.
Men kanske mest av allt hade jag i livet behövt vara omkring människor som känner till min problematik, så att de inte oavsiktligt skadar mig.
Men det är bara teori, tankar om vad som hade kunnat undvika den här utvecklingen de senaste två årtiondena. Nu står jag här och måste hantera situationen själv. Jag har dock ingen som helst idé om vad jag skall göra.
Om någon av mina omkring 0 läsare har en idé, så får han eller hon gärna höra av sig.
Det upprivna såret blev droppen som fick bägaren att rinna över. Jag blev inlagd på sjukhuset söndag morgon, men blev ofrivilligt utskriven under måndagen.
Men jag fixar inte det här själv. Jag kan inte leva med all smärta och inget hopp om lindring inom en rimlig framtid. Jag har inte ens en plan för hur jag skall hanterar stressorerna omkring mig.
Jag har gång på gång överlevt kriserna de senaste 20–30 åren, men jag orkar inte mer. Jag vill inte överleva: jag vill leva, eller, om det inte går, få dö.
I går publicerade jag en artikel om kommunikation och empatiskt bemötande när tunga ämnen kommer upp.
Efter att jag skrivit den artikeln hände något tråkigt.
Av en slump visar det sig att flera av artikelns mer generella nyckelord kan användas för att förstå det tråkiga som hände mig i går, även om händelsen inte alls har något med artikelns huvudsakliga scenarion att göra.
I artikeln pratar vi om att olika människor har olika behov för att må bra. I mitt fall känns det som om det med tiden blivit allt tydligare vilka dessa behov är:
Jag vill inte leva ensam. Jag behöver en bästa vän att komma hem till på eftermiddagarna och vara tillsammans med under min lediga tid. En social, trygg, vuxen och levande person. Någon att dela livet med.
Jag behöver en sysselsättning som jag verkligen brinner för och som är ”mer” än bara ett jobb. Jag hade det i naturvetenskapen och matematikundervisningen förra årtiondet, och höll sedan på att hitta det igen i medicinen och läkarrollen, men jag tvingades som bekant ge upp båda banorna.
Jag tror att jag skulle må bra i en livssituation med bara en av dessa fördelar. Men nu har jag ingen av dem, utan i stället PTSD och en hel del annan ohälsa och dåligt bearbetade trauman efter läkarprogrammet och tidigare. Det är väldigt tufft. Min stressnivå är alldeles för hög och nästan konstant. Allt för sällan händer något riktigt roligt.
Vi pratade i artikeln också om att olika människor har olika förutsättningar för att klara av livets prövningar. I mitt fall kan man konstatera att min förmåga att påverka min livssituation är mycket dålig. Det finns saker jag är bra på: kommunikation¹, matematik, naturvetenskap, programmering, att vara lärare, att lyssna på människor, att prata om känslor. Men när det gäller att framhäva sig själv – t.ex. på arbetsmarknaden – eller ta för sig – t.ex. i sociala sammanhang –, då hamnar jag efter nästan alla andra. Sådant har jag alltid varit dålig på, och med bagaget från LiU (juridiskt, psykologiskt, bakgrundsmässigt) har jag nästan inga chanser alls.
Det som hände i går var att ett gammalt sår, relaterat till behoven ovan, revs upp.
Jag märkte under kvällen att jag påverkats ganska mycket. Natten blev sömnlös, och i dag hade jag för mycket oro och ångest för att kunna arbeta. Det känns nästan som en depression.
Det var personer i min omgivning som helt oavsiktligt rev upp såret. De hade ingen som helst möjlighet att ana något problem, ingen som helst anledning att agera annorlunda. Inte på något sätt är jag arg eller besviken på dem: man kan inte vara arg på någon som gjort precis allting rätt.
Om man kan säga något om händelsen är det väl snarare att den utgör ytterligare ett bevis på att min aktuella livssituation inte är stabil, något som jag länge varit mycket väl medveten om. Det skall inte vara så här lätt för någon att oavsiktligt orsaka stress och oro hos en annan person.
Möjligtvis finns ett litet ”men”: För en person som känner mig tillräckligt väl hade det varit uppenbart att gårdagens händelse riskerade att riva upp sår. Kanske borde jag vara mer öppen om min bakgrund (också ett nyckelord från artikeln), så att personer omkring mig är medvetna om den, och därmed, bland annat, har möjlighet att undvika att riva upp sår som det här? Det är en fin tanke, men det är svårt i praktiken. Min bakgrund är så komplicerad att den är ytterst svår att förklara. Jag har försökt skriva en bok, men vem orkar läsa den? Och hur sammanfattar man den på en minut? Jag vet inte om jag kan det.
Det ligger i gårdagens händelses natur att den kan upprepas. Jag skulle vilja trycka på ”Paus” på livets fjärrkontroll – ”nu blev det för otäckt, nu vill jag inte se mer”. Men det går inte. Tiden kommer att fortsätta framåt vad jag än gör.
Jag får försöka täcka såret med plåster och bandage. Och absolut inte klandra någon.
¹ Men helt klart inte tillräckligt bra.
När man pratar med människor – eller bara befinner sig bland människor – är det viktigt att man är observant på de signaler de sänder ut.
I synnerhet är det viktigt att man lägger märke till om något tyngre ämne kommer upp.
Det kan handla om ett dödsfall, om allvarlig sjukdom eller olycka, om en personlig tragedi, om en livskris. Men det kan också röra sig om något som vid en första anblick kanske inte alls låter särdeles traumatiskt, men som ändå är en väldigt stor sak för personen i fråga. Alla är vi ju olika: vi har olika förutsättningar för att klara av livets prövningar och vi har alla våra egna rädslor och behov. Ibland behöver man därför även lyssna mellan raderna för att se tyngden. Man kan också behöva dra sig till minnes vad man vet om personens bakgrund, tankesätt och farhågor.
När man märker att ett tungt ämne kommer upp är det viktigt att man anpassar sitt eget beteende till situationen.
Man måste visa att man ser det tunga, att man tar personens problem och oro på allvar, att man verkligen försöker förstå hur hon upplever det. Man bör prata lugnt och med mild röst, med stor eftertänksamhet. Man måste välja sina ord väl för att ge tröst och – om det ens är möjligt – bidra med någon ny infallsvinkel. Med kroppsspråket, framför allt ansiktsuttrycket, kan man förtydliga sin kommunikation och visa medkänsla.
Ibland behövs en tvär omställning. Kanske var man mitt uppe i en livlig och lättsam diskussion med andra personer när det tunga ämnet kom upp. Då gäller det att utan fördröjning gå över till det nya läget.
I en del fall märker man att ett tungt ämne kommer upp i ett samtal mellan två personer i ens närhet, även om man själv inte är direkt involverad. Även då är det viktigt att man anpassar sig och inte är okänslig. Det är t.ex. inte läge att avbryta deras samtal för någon trivialitet.
Jag har flera gånger sett när personer misslyckas med det här. Det leder inte till något gott.
Efter att jag publicerat artikeln om vinterns sjukdomar insåg jag att listan över en övre luftvägsinfektions konsekvenser saknar en viktig punkt: nedsatt röstfunktion gör det inte bara svårt att sjunga, utan också att effektivt kommunicera i vanligt tal.
Det jag då främst tänker på är inte det uppenbara: svårigheter att producera ljud som kan tolkas som ren text, som en grammatiskt korrekt följd av ord. Den förmågan försvinner sällan helt.
Det jag i stället tänker på är förmågan att i talet variera röstläget – tonhöjd, melodi och rytm – för att på så sätt säga mycket mer än vad som framgår av orden och meningarna i sig. Det är ju onekligen så att det sätt på vilket man säger något påverkar hur mottagaren tolkar meddelandet. Röstläget – och kroppsspråket – kan ersätta åtskilliga meningar av förtydligande text.
Tänk bara på ett enkelt ”hej” eller ”god morgon”. Man kan uttala det kort och monotont, men man kan också frambringa interjektionen på ett sjungande sätt, och på så sätt förmedla information som annars inte alls hade varit uppenbar:
”Jag är snäll, jag bits inte, jag är tillgänglig.”
”Jag är på bra humör.”
”Jag tycker det är roligt att se dig.”
Ibland också ”Du är en betydelsefull person [för mig].”
(Det är dock svårare att sjunga på korta, enstaviga ord: det finns då inte så mycket man kan variera. När jag väl tänker efter inser jag t.ex. att jag själv alltid säger ”Hallå!” i stället för ”Hej!” och ”Ja-a” i stället för ”Ja”, med den första stavelsen i ett högre tonläge.)
Ett annat exempel är om man behöver rätta en annan person, när hon gör något på fel sätt, t.ex. i ett yrkesmässigt sammanhang. Då kan en mild röst förmedla saker som:
”Jag är inte arg.”
”Det är inte så viktigt, men […]”
”Ingen fara. Ingen skada skedd.”
”Det är lätt hänt.”
I sådana situationer kan det också vara en god idé att lägga till mildrande budskap i själva texten. Jag brukar använda mig av följande formuleringar:
”Det är (kanske) inte jätteviktigt, men (jag tror) det är bättre om vi/vi brukar […]” (om lämpligt följt av en förklaring till varför det är bättre)
”Egentligen ska/borde […], men det här går bra också (men nästa gång...)”
”Det gör inget, men du borde ha/vi brukar […]”
”Det är mitt fel – jag borde ha sagt till dig tidigare – men […]”
Grundregeln är att det aldrig händer något dåligt om man är ”för” mild eller snäll eller ödmjuk. Däremot kan det hända dåliga saker om man är för hård.
På ett betydligt mindre subtilt plan behövs också förmåga till variation i rösten för att förmedla betydelseförändrande emfas:
Katten är min. (Inte hunden!)
Katten är min. (Jag menar det verkligen!/Jag skojar inte!)
Katten är min. (Inte din!)
Samtliga meningar säger att ”katten är min”, men lägger till olika information om vad utsagan skall ställas i kontrast mot. Här rör det sig om en form av röstvariation som har en motsvarighet skriftspråket, i form av kursivering (och i hypertext, i form av em-noder).
Slutligen bör nämnas att det inte bara är röstläget som kan lägga till förklaringar och känslor till orden, utan även kroppsspråket. Ansiktsuttrycket, som förmedlas av de otaliga musklerna i ansiktet (de mimiska musklerna), spelar en otroligt stor roll i hur budskapet upplevs. Lutningen på huvudet, kroppshållningen i övrigt, var händerna finns, hur man står/sitter, spelar också roll.
I synnerhet om man lyssnar på en människa som berättar om något sorgligt, tragiskt eller otäckt, är det fullkomligt avgörande vad man säger mellan raderna i sitt gensvar. Rösten bör vara mycket mild, ansiktsuttrycket bör tydligt återspegla de känslor som slår emot en. Både mellan och på raderna är det viktigt att man bekräftar (och tröstar).
Över lag tror jag att människor lägger för lite vikt på det som står mellan raderna vid muntlig kommunikation. Jag minns t.ex. de läkare jag träffade under traumat på läkarprogrammet (både som representanter för läkarprogrammet och behandlande läkare): Många stela robotar. Det förvärrade situationen.
Det är när man är sjuk och inte kan sova på nätterna som man upptäcker nya sidor av sitt hem, som t.ex. skådespelet i taket i vardagsrummet:

Förra veckan kunde jag inte sova för den mycket intensiva hostan. Den här veckan ser det ut att bli smärta i rygg och nacke som håller mig vaken om nätterna.
Jag tycker väldigt illa om vintern i Sverige:
Den främsta anledningen är den ökade förekomsten av smittsamma virus under vintern, framför allt virus som orsakar övre luftvägsinfektioner samt virus som orsakar akut gastroenterit (läs: calicivirus1). Jag har de senaste åren utvecklat en patologisk rädsla för sådana virus.
Det är mörkt. Jag påverkas mycket av omgivningen omkring mig. Vackra miljöer, sol och grönska har en positiv inverkan; mörker och slaskväder har en negativ inverkan.
Det är kallt och allmänt otrevligt att vistas ute.
Den mest intressanta punkten är den första, så låt mig skriva lite om den.
Det är förmodligen flera faktorer2 som ligger bakom min fobi för vinterns patogener:
Från högstadiet och fram till och med läkarprogrammet betydde matematiken och naturvetenskapen allt för mig. Det var min passion i livet. Nu har jag förlorat den, när jag först tvingades sluta som lärare i matematik och sedan tvingades sluta som läkarstudent. Detta lämnade ett enormt tomrum hos mig – jag vet knappt vem jag är längre. Jag försökte fylla tomrumet med sång, och övre luftvägsinfektioner utgör ett mycket stort hot, om än inte permanent, mot talapparaten.
De diffusa mun- och halsproblem med oklar bakgrund som jag haft sedan januari i år har gjort mig extra nervös (paranoid) inför den orofaryngeala slemhinnans hälsa.
Jag är mycket mån om att alltid göra ett ”snyggt” intryck (lite som om jag vore den brittiska drottningens butler), och det är svårt om man har snuva, hes röst3, hosta och allmän irritation i halsen.
Jag är väldigt mån om att aldrig skada eller stressa andra människor, och när man är sjuk riskerar man att smitta andra. Dessutom, om man har symtom riskerar man att stressa upp andra som är rädda för att bli smittade. (Jag själv blir numera mycket stressad om jag anar förekomst av förkylningsvirus eller calicivirus i min fysiska närhet, även om jag gör mitt bästa för att det inte skall synas. Och jag tror att den här typen av rädslor är hyfsat vanliga i i-länder.)
Men den kanske största bakomliggande orsaken är att jag numera mår väldigt dåligt över lag, både själsligt och kroppsligt (hals, höft, …), och ofta funderar på hur länge jag kommer att orka fortsätta. Då känns det som om en ytterligare påfrestning – som t.ex. en virusinfektion – är långt ifrån vad jag skulle behöva.
I mer abstrakta termer antar jag att min förmåga till coping är kraftigt nedsatt. Dels har vi PTSD:n efter traumat på och efter läkarprogrammet och universitetets rättsprocess mot mig (där jag inte fick någon chans att försvara mig), dels har vi min känsla av att inte ha någon framtid. Trots allt ser det ut som om jag aldrig kommer att få välja vare sig min livssituation eller mitt yrke själv. LiU satte i praktiken den sista spiken i kistan vad gäller mina fåfänga drömmar om att bli matematiklärare, läkare, pilot, … . Det är tråkigt, eftersom jag har svårt att leva utan någon sysselsättning som jag verkligen brinner för. Min hjärna funkar inte då.
Mina mycket noggranna hygienrutiner har emellertid inte haft någon imponerande effekt under hösten: jag har nu drabbats av min andra infektion med feber och halsont.
Jag verkligen avskyr den svenska vintern.
1 Jag har slutat titta på Folkhälsomyndighetens (f.d. Smittskyddsinstitutets) calicivirusrapporter. Det enda som händer är att jag blir mer stressad av det.
2 Privatpersoner, myndigheter och media tycker om förenklingar, men i verkligheten torde de flesta fenomen bäst beskrivas som multifaktoriella. Det är sällan jag numera tycker det känns rätt att säga att en ensam omständighet ligger bakom någon företeelse. Kanske beror den förändringen hos mig också på att jag numera funderar mycket mer på humanistiska frågor än på naturvetenskapliga.
3 Att påpeka att jag har hes röst vid en infektion är behäftat med viss fara för ett kortfattat svar från min sida, för jag är numera alltid så otroligt upprörd själv över det, och känner därmed inte för att få det bekräftat eller upprepat. Så ett tips är att i stället säga något i stil med ”vilken kraftfull röst du har i dag!”.
Höften har inte fungerat som den ska de senaste veckorna.
När jag promenerade hem sent på kvällen den 3 november kände jag av en viss smärta på vänster sida. Jag har haft ont i höften tidigare, så jag tänkte inte mer på det.
Under natten gjorde det emellertid så ont att jag inte kunde sova. Det är då man vill få i sig lite paracetamol och NSAID. Problemet var att jag hade tabletterna i köket, och för att komma från sovrummet till köket behöver man en fungerande höft. Varje belastning av höften – faktiskt varje rörelse – orsakade intensiv smärta, så det tog mig åtskilliga minuter att komma till köket. Jag fick luta mig mot väggarna och försöka ta mig fram genom att hålla i dörrhandtag, bänkar och annat som jag fick tag på. Det svåraste var att komma från ena sidan av köket till den andra, för då var jag tvungen att tillfälligt stödja mig på vänster ben.
När jag väl fått i mig tabletterna var det dags att gå tillbaka, och då fastnade jag mitt på golvet, stående på höger ben, och jag vågade inte röra mig ur fläcken av rädsla för att falla ihop om jag försökte sätta ner vänster ben. Till slut blev jag så trött i höger ben att jag riskerade att falla ihop ändå. Då trotsade jag smärtan och lyckades långsamt ta mig tillbaka till sängen utan någon olycka (aj, vad ont det gjorde).
Dagen efter hade smärtan lättat något, men jag kunde ändå inte promenera i normal takt. Vanligtvis går jag till och från jobbet och restaurangen i hög fart, men nu lyckades jag bara komma upp i kanske 20 % av normal fart, kraftigt haltande. Dumt nog valde jag ändå att promenera både till jobbet och till restaurangen. På kvällen blev smärtan mycket intensiv, även när jag höll höften helt stilla, så jag kunde inte sitta på restaurangen utan fick ta en taxi hem.
Jag lade mig i sängen, och blev där liggande. Jag försökte ta mig ur sängen, men lyckades inte: smärtan när jag rörde höftleden var för stor.
Efter 18 timmar ringde jag efter ambulans. De hjälpte mig ur sängen och körde mig till sjukhuset på en bår.
Undersökningen på sjukhuset gav inga nämnvärda fynd, så jag skickades hem med mer paracetamol och NSAID och en remiss till sjukgymnast.
Natten därefter fastnade jag i sängen igen. Jag behövde kasta vatten, och visste inte vad jag skulle ta mig till. Efter en stor mängd smärta (och en del läckage i samband med smärtan) kom jag till toaletten och fick tömma blåsan. Men sedan skulle jag ta mig upp från toalettstolen, och det är en väldigt krävande uppgift. Smärtan – och rädslan för smärta – gjorde att jag blev sittande länge.
De kommande dagarna blev det långsamt bättre, men sedan planade det ut.
De senaste två veckorna har ingen förbättring skett. Smärtan är inte längre intensiv, men den är nästan alltid närvarande vid belastning. Det gör ont när jag går, böjer mig ner, vänder mig i sängen, reser mig upp o.s.v. En del dagar kan jag inte promenera alls, andra dagar går det bra men i lägre fart och med en haltande gångstil. Kanske är det haltandet som gjort att jag nu också fått ont i nacken.
Sjukgymnasten hittade inget uppenbart fel på höften, så min förhoppning är att det kommer att bli bra av sig självt inom några veckor eller månader.
Trots allt känns det som om höften är ett av mina mindre problem.
De halsproblem som först uppträdde i mitten av januari i år försvann aldrig riktigt: jag har sedan dess nästan dagligen känt av obehag från munhåla och svalg.
Jag vet inte vad problemen beror på, men det verkar troligt att en betydande psykosomatisk komponent föreligger. Under året har jag varit konstant stressad. Det har tagit och tar otroligt mycket energi att hantera PTSD:n från läkarprogrammet och känslan av hopplöshet och allmän meningslöshet.
Dessutom kan sången ha haft en negativ inverkan på den upplevda orofaryngolaryngeala hälsan, men kanske inte på det sätt man skulle kunna tro (fysisk påfrestning av talapparat). Sedan jag började sjunga har jag nämligen oroat mig väldigt mycket för hälsan i svalg och talapparat och t.ex. blivit väldigt rädd för alla former av virus som kan infektera de övre luftvägarna.1 Den här oron kan – ironiskt nog – ligga bakom en del av problemen.
I den mån intensiteten hos halsproblemen har korrelerat med något så har det varit med nivån av sysselsättning: vid de få tillfällen jag har varit fullt sysselsatt med något spännande har jag ofta helt glömt bort halsen. Men större delen av tiden har jag varit ganska rejält uttråkad, och då har halsen gjort sig påmind. Jag tror det har varit värst på måndagarna: ibland har jag nästan haft svårt att andas. Möjligtvis har det då rört sig om lättare ångestattacker.
Den intellektuella tristessen har under året förvärrats något av det faktum att jag numera nästan aldrig är hemma och därmed ytterst sällan kan syssla med sådant som jag gjorde förr i tiden: utveckla mjukvara privat, skapa matematisk konst, skriva artiklar, skapa ordboksartiklar, se på film, läsa böcker. Nu går jag till jobbet tidigt på morgonen och kommer hem från restaurangen sent på kvällen, så det enda jag gör hemma är i princip att sova. Det blev så här i vintras och i våras: jag var så otroligt rädd för att upptäcka post från Linköpings universitet eller någon domstol att jag inte vågade gå hem från restaurangen på kvällarna.
Antagligen är det också stressen som ligger bakom den relativt stora viktminskningen efter läkarprogrammet (kanske 15–20 kg). Jag räknas numera som underviktig med ett BMI strax under 18.
Så även om halsproblemen kan ha en viss fysiologisk bakgrund så är det nog i hög grad psykologiska mekanismer som är verksamma. Skulle jag t.ex. mirakulöst komma in på Trafikflyghögskolan (eller om något annat riktigt roligt skulle inträffa, så att jag också blir sysselsatt och får en känsla av mening och av en framtid), skulle antagligen vikten gå upp och halsproblemen förpassas till historien.
1 Det här kan låta märkligt, men man får beakta omständigheterna: från början höll jag på med matematik och naturvetenskap, och de betydde allt för mig i livet. Sedan tvingades jag sluta med det, och försökte bygga upp ett nytt liv inom medicinen. Så tvingades jag sluta med det också. Med sången försökte jag desperat hitta något nytt att leva för.
Jag mottog i fredags med posten ett brev från Högsta förvaltningsdomstolen. Jag har lagt brevet på en plats där jag inte ser det. Tidigare har sådana brev nästan utan undantag lett till att polisen kört mig till sjukhuset, att jag skurit mig i armarna eller ännu värre. Men det behöver inte bli så den här gången. Det är ingen som vet.
Det kan hända att jag öppnar det på onsdag eftermiddag. Då har jag lite extra stöd runtomkring mig.
Uppdatering (2019-09-30 23:43): Jag öppnade kuvertet under onsdagskvällen. Jag fick under kvällen och dagarna efter otroligt mycket stöd av och kärlek från människorna omkring mig. Det är något jag inte är van vid sedan tidigare, och jag känner mig väldigt tacksam, rörd och lite överväldigad.
Människor har lätt för att döma.
De hittar någon ”dålig” egenskap hos en annan person och förlorar sedan, via psykologiska mekanismer, större delen av sympatin för henne och viljan att hjälpa henne.
”Det inte synd om henne eftersom hon X. Då får hon skylla sig själv.”
”Jag tänker inte hjälpa henne så länge som hon Y.”
”Hon måste sluta med Z, annars är hon inte välkommen här.”
Hur många gånger har jag inte hört sådana kommentarer.
Jag tror att det nästan alltid handlar om bristande förståelse hos den som dömer.
Om personen som dömer fick pröva att leva i den dömdas situation skulle hon kanske inse att allt inte var så enkelt som hon trodde. Kanske skulle hon inse hur hemsk situationen som den dömda hamnat i faktiskt är, vilket enormt lidande den kan innebära och hur otroligt utsatt den dömda är. Kanske skulle hon förstå att den dömdas till synes ”dåliga” agerande är fullt förståeligt eller rent av välmotiverat eller oundvikligt (t.ex. av medicinska orsaker). Kanske skulle hon själv agera precis likadant – eller ännu ”värre”.
Det är lätt att döma när man inte vet vad man pratar om.
Hur upprörd jag blir när jag hör kommentarer av den här typen beror på hur utsatt den dömda ser ut att vara. Om hon är en stark och självständig person med mycket skinn på näsan, en fungerande livssituation som hon trivs i, ett fungerande socialt nätverk, fungerande skyddsnät o.s.v. så bekommer kommentarerna mig inte, åtminstone inte så länge den som dömer besitter ringa eller måttlig makt över den dömda.
Om kommentarerna däremot riktar sig mot en person som jag ser är utsatt och ensam och i behov av stöd och hjälp från sin omgivning, så kan jag bli riktigt upprörd. Faktiskt är det få företeelser som kan få mig argare.
Mot slutet av min sista termin på läkarprogrammet, den där hösten 2016, mitt under den värsta krisen, hade jag en del kontakt med några få klasskamrater.
Jag minns att jag fick ett sms från en av dem. Han föreslog att jag skulle tänka på Jesus och söka tröst i hans berättelse.
Jag hade alltid varit en renodlad naturvetare i själ och hjärta, med den vetenskapliga metoden sedan barnsben hårdkodad i storhjärnsbarken, ovillkorligen negativt inställd till all form av religion, vidskepelse och pseudovetenskap. Så jag kände en viss tveksamhet inför sms:et. På ett etiskt plan tyckte jag också det var aningen tveksamt att bemöta en sårbar människa i kris med religiös propaganda, även om jag förstod att han bara hade goda avsikter.
Men jag blev ändå inte nämnvärt upprörd och en av anledningarna var att jag faktiskt fann en tröst i Jesus berättelse.
På grund av min neuropsykiatriska variation hade jag vuxit upp i princip helt utan vänner, med årtionden av svår depression och ångest som följd.
Jag hade aldrig haft någon att prata med, eftersom ingen tog problemen på allvar – den typen av problem som jag hade ”finns inte” i Sverige, ingen har hört talas om sådant. Jag hade heller inte på långa vägar några förutsättningar för att lyckas med att bilda familj och i praktiken dåliga förutsättningar för komma dit jag ville yrkesmässigt. För att lyckas på arbetsmarknaden räcker det ju inte med toppbetyg och yrkeslämplighet – man behöver armbågar, en förmåga att inte beskriva sig själv 100 % objektivt, en bakgrund som inte inger osäkerhet, en ork att byta livssituation, ett mod att överge de invanda dagliga rutinerna.
Jag ville alla väl på läkarprogrammet, var övertydlig med det, och en betydande del i min akuta kris den hösten var mitt engagemang för en utsatt släkting i en släktkonflikt, men jag blev bemött av förakt och fördomar av lärarna på läkarprogrammet. Tillsammans med universitetets rektor författade de sida efter sida med text, som utmålade mig som en dålig människa utan självinsikt och empatisk förmåga, som utgjorde en fara för sin omgivning. Allt snyggt och proffsigt formaterat på Linköpings universitets officiella brevpapper. Det objektiva underlaget för deras utsagor var mycket oklart, och texterna innehöll åtskilliga osakligheter och en del rena faktafel. Deras mål var att få mig portad från all svensk högskoleutbildning, till synes av politiska eller ideologiska skäl eftersom jag redan hoppat av utbildningen när de skickade in sin anmälan till HAN. De ville slå in sista spiken i kistan för mina fåfänga drömmar att komma någonstans i livet.
Med tanke på det otroligt dåliga skick jag befann mig i hade jag behövt mycket värme, stöd och hjälp från LiU och klasskamraterna, men fick i stället mottaga förakt och fick stora, livsavgörande, rättsliga åtgärder mot mig. Hela mitt sociala sammanhang, min självkänsla och allt framtidshopp togs abrupt ifrån mig när jag var som svagast. Det är ett recept på att ta död på en människa.
Under vintern påbörjades en plågsam rättsprocess som pågår än i dag, tre år senare. Jag har tappat räkningen på hur många gånger polisen hämtat mig när de varit rädda för suicid och stressen för min familj har varit omänsklig. Det går inte en timme utan att jag plågas av minnesbilder av det som läkarna och rektorn och klasskamraterna skrev och sade, och det tar otroligt mycket energi från mig att hantera PTSD:n och dess följder.
Tillbaka till hösten 2016: Mitt i all hopplöshet och förtvivlan kändes det tryggt att tänka på Jesus, som fått utstå en ännu större prövning. Jag var inte ensam. Även formuleringar som ”Gud ger de största prövningarna till sina starkaste soldater” skänkte en viss tröst. Det är fascinerande att den kristna tron kan ge så mycket även för en icke-troende. Det säger något om styrkan i religionen, om inte annat än för coping.
Under hösten och vintern var det några få klasskamrater som uttryckte förvåning över universitetets agerande och tog kontakt med mig. Nästan samtliga av dessa var antingen troende kristna eller med utländsk bakgrund. Man kan undra varför, och jag har en del hypoteser (som jag skriver om i Ändlös längtan). Under 2018 sökte jag mig alltmer till den vackra domkyrkan, där jag fick prata med präster och diakoner när hopplösheten och förtvivlan höll på att ta död på mig, typiskt efter att jag mottagit brev från LiU eller någon domstol. Det var väldigt känslosamma och fina möten.
Det må så vara, att naturvetarna har bättre koll på hur universum och naturen fungerar, medan de religiösa lättare får för sig saker som kanske inte riktigt (eller alls) stämmer. Men vad betyder faktamässig korrekthet om man tappat förmågan att se människan och bemöta henne med värme och respekt? Det betyder inget.
Hösten 2018 gick jag med i Svenska kyrkan.
Jag är för närvarande inte en aktiv medlem. Jag har knappt besökt domkyrkan på över ett halvår. Anledningen är att jag har andra platser (eller, rättare sagt: en annan plats) att vara på, som är så bra att jag inte känner något behov av att vara någon annanstans. Men jag är ändå glad över att jag nu är medlem, och kanske blir jag mer aktiv i framtiden.
Att leva är som att befinna sig alldeles ensam i vattnet mitt ute på havet.
Man klamrar sig desperat fast vid de få livbojar man hittar och är ständigt orolig för att bojarna som för stunden håller en uppe skall gå sönder och börja sjunka.
Något som inte alla förstår är att en del av bojarna i vattnet inte förmår hålla en flytande, trots att de ser helt dugliga ut. Man skäms och känner sig otacksam när man överger en sådan boj, men man har inget val.
Ingen boj skänker emellertid evigt liv. Man är väl medveten om att man en dag kommer att tappa taget och sjunka till havets botten. Kanske i morgon, kanske om tio år.
Till dess stannar man vid sina bojar.
(Det man inte förstod var att havet var en bassäng. Man hade när som helst kunnat ställa sig på golvet och ha huvudet ovanför vattenytan.)
Ofta är en persons mentala ohälsa inte märkbar för hennes omgivning, annat än för de allra mest observanta. Och även om någon kan ana ohälsan, så är det stor risk att hon underskattar dess omfattning och vidden av dess konsekvenser för den drabbade. Lidandet kan vara hur stort som helst, utan att det syns.
Därför är risken stor att den drabbade inte får den hjälp och det stöd hon behöver av människorna omkring henne.
Något som däremot syns mer än väl är de konsekvenser som ohälsan kan ge upphov till. Det är inte ovanligt att en person som lider av mental ohälsa inte lyckas leva upp till alla förväntningar som hon har på sig, vad gäller arbetet, familjen, bekanta. Det blir sjukfrånvaro, sämre prestationer, saker blir inte gjorda, personer känner sig försummade av henne.
Då är det lätt hänt att omgivningen reagerar med besvikelse och ilska – men inget kunde vara mer oändamålsenligt.
I stället för att klandra personen för de tre sjukdagarna borde man hylla henne för att hon orkade med de tio andra dagarna. Kanske har hon under dessa dagar utfört sina plikter trots en ångest och en oro och en trötthet som ingen annan ens kan föreställa sig. Kanske hade de som klandrar henne inte förmått arbeta någon av dessa dagar under likvärdiga förutsättningar.
Varje människa med mental ohälsa förtjänar en guldmedalj för allt hon orkar med!
Fortsättning på artikel 506.
I BBC:s värdefulla inslag om sexköp för funktionsnedsatta betonades de funktionedsattas utanförskap och utsatthet – och deras behov av fysisk närhet. En av de intervjuade personerna förklarade att ”[t]here are some parts of you that do die” om du permanent lever i utanförskap vad gäller fysisk närhet. Inslaget präglades över lag av medmänsklig värme och av en förståelse för såväl den mänskliga situationen som för samhällets ansvar för de utsatta – på ett sätt jag aldrig sett i svensk media.
En bidragande faktor för mitt engagemang i frågan är så klart min egen bakgrund.
Som framgår av min biografi och boken Ändlös längtan gjorde min neuropsykiatriska variation att jag växte upp nästan helt utan vänner och i synnerhet helt utan någon fysisk närhet.
Redan på lågstadiet visste jag att mina chanser att få en partner var i praktiken exakt noll. Detta ledde till ett enormt utanförskap och lidande under hela uppväxten, svår depression och daglig ångest som snart gjorde vardagen ohållbar och skulle få enorma konsekvenser för mitt fortsatta liv. Det svåraste var att leva i ett samhälle där ”alla andra” hade vänner och partners, och där ”ingen” visste om att det fanns folk som levde i utanförskap.
Rent kliniskt rörde det sig helt klart om ett trauma av kolossal magnitud. Men det var inte ett av de trauman som samhället kände till. Om en person utsätts för långvariga sexuella övergrepp som barn, blir traumatiserad av en uppväxt i en krigszon, förlorar sitt barn i cancer eller blir utsatt för eller får bevittna tortyr, så förstår alla de psykologiska konsekvenser som detta orsakar. Samhället och sjukvården förstår hur allvarligt det är och vet att resurser måste sättas in – ibland finns till och med specialistkompetens för aktuell problematik.
Men ingen hade hört talas om att ”brist på flickvän” (en populär men väldigt onyanserad sammanfattning av problematiken) kunde ge några men för livet. Ingen i min närhet förstod hur stort traumat var för mig, vilka men det hade gett och skulle ge, hur stor den kliniska betydelsen av traumat skulle bli. Dels gjorde detta så att jag inte fick någon hjälp, trots att jag var helt öppen med mina problem sedan högstadiet/gymnasiet, dels utgjorde samhällets nonchalans ett trauma i sig.
Jag inbillar mig att mitt liv hade kunnat se helt annorlunda ut i dag (som det är nu tampas jag dagligen med svår ångest, PTSD och OCD, i synnerhet efter LiU:s behandling av mig) om samhället hade förstått och lyssnat. Tänk om någon under högstadiet hade sagt till mig ”Gud, vilket liv du har levt. Jag förstår hur enormt mycket du har lidit. Men vet du vad? Vi [t.ex. BUP] skall göra allt vi kan för att hjälpa dig, och vi har experter på området.”
En annan sak som jag tror hade kunnat förhindra den totala urspårningen hade varit ifall sexköp varit lagligt i Sverige, åtminstone för personer med läkardiagnosticerad oförmåga att på egen hand skaffa vänner eller fysisk närhet.
Alldeles för sent (förra året, 2018), åkte jag till Danmark och fick träffa jämnåriga kvinnor som jag fick en del fysisk närhet av. Det rörde sig mest om kramar och handhållning, eftersom ”mer avancerad” fysisk närhet både är något jag ogillar och något som vore alldeles för svårt för mig. Och nu, ett år senare, märker jag att den känsla av utanförskap som sedan förskoletiden orsakat så otroligt mycket lidande för mig, inte finns längre. Danmarksresorna är nästan säkert en av de två omständigheter som ligger bakom denna förändring.
Hade det svenska samhället (1) visat förståelse och empati för mina problem redan under skoltiden och (2) lett mig till säker och trygg fysisk närhet vid första möjliga tillfälle, är jag nästan övertygad om att urspårningen hade kunnat undvikas. Kanske hade jag i dag varit en frisk och lycklig människa, väl integrerad i det svenska samhället, kanske som matematiklärare eller som läkare.
Jag hoppas innerligt att det svenska samhället någon gång
kommer att förstå att den sorts problematik som plågade mig under hela min uppväxt och mitt tidiga vuxenliv faktiskt kan utgöra ett enormt trauma
kommer att förstå att denna problematik inte är något som personen ifråga själv har valt och inte på något sätt innebär att han eller hon är en ”dålig” människa
kommer att kunna visa empati och stötta personer med den typen av problematik, t.ex. genom en attitydförändring, bättre kunskap och – eventuellt – legalisering av givande av fysisk närhet under trygga, säkra och motiverade former.
Jag betvivlar emellertid att jag kommer att få se en sådan attitydförändring i Sverige under min livstid.
Bakgrund: Om sexköp, Ändlös längtan.
Jag brukar inte kommentera inslag och artiklar i media. Oftast har jag inget att säga, eller så suckar jag tyst för mig själv när jag läser en nyhetsartikel där det märks att författaren har en tydlig politisk färgning och bara visar ena sidan av myntet. Framför allt SVT brukar publicera artiklar där den rådande svenska politiska agendan är övertydlig, vilket antagligen är uppenbart för de flesta icke-svenska läsare.
Brittiska BBC håller högre kvalitet och det är deras media jag konsumerar mest av.
Och i dag fick jag syn på ett BBC-inslag som verkligen fick mig att höja på ögonbrynen. Inslaget handlar om hur funktionsnedsatta i Storbritannien har möjlighet att köpa sexuella tjänster.
I inslaget pratas det om de funktionsnedsattas utsatthet, livssituation och utanförskap – och om deras behov av närhet. Inslaget diskuterar sexköp utan att döma vare sig utövare eller kund. Det är inte på långa vägar något tal om att sexarbetaren blir utnyttjad. I stället slås jag av den värme och förståelse som den intervjuade sexarbetaren och andra i inslaget visar gentemot de funktionsnedsatta klienterna.
En intervjuad sexterapeut har följande att säga:
Someone could make an incredibly powerful argument that this is a basic human right. Ok, you don’t die from a lack of sex like you do from a lack of food and water, but really? There are parts of you that do die. […] I think if people are unable to do certain things in society, then society should take a corporate responsibility to help.
Det här är ett ämne som SVT aldrig skulle ta upp på samma sätt. Om SVT skulle ta upp något liknande så skulle det heta att de funktionsnedsatta är dåliga människor som utnyttjar utsatta kvinnor och att samhället måste få ett stopp på det. Antagligen skulle de visa bilder på en polisinsats mot sexköp.
En av de få sympatiska läkare jag träffat det senaste året nämnde att även Danmark har en liknande syn på sexköp till funktionsnedsatta.
Jag hoppas att Sverige någon gång kommer att komma ikapp Danmark och Storbritannien.
Bakgrund: Om sexköp, Ändlös längtan.
Läs mer i artikel 507.