(Den här artikeln innehåller matematik. Du behöver en modern webbläsare med stöd för MathML, t.ex. Mozilla Firefox, för att visa den korrekt. Om du inte har en sådan webbläsare kan du i stället läsa artikeln i PDF-format.)

Hur fungerar spegelsimulatorn, d.v.s. hur beräknas riktningen hos de reflekterade strålarna?

Situationen är följande: vi har en given yta $S\subset {\mathbb{R}}^3$ och en given punkt $P\in S$. Mot denna punkt infaller en ljusstråle, den inkommande strålen, med given normerad riktningsvektor $\widehat{\mathbf{i}}$. Denna stråle reflekteras, och problemet består i att beräkna (den normerade) riktningsvektorn $\widehat{\mathbf{r}}$ för den reflekterade stålen, som alltså kan parametriseras $P+t\widehat{\mathbf{r}}$ med $t\ge 0$.

Den fysikaliska lag som är relevant här är reflektionslagen, som säger att

1. den inkommande strålen, ytans normal i punkten och den reflekterade strålen ligger i samma plan
2. vinkeln mellan den inkommande strålen och normalen (infallsvinkeln) är lika stor som vinkeln mellan normalen och den reflekterade strålen (reflektionsvinkeln).

I bilden nedan är den inkommande strålen vit, liksom dess normerade riktningsvektor $\widehat{\mathbf{i}}$ som pekar mot $P$; normallinjen är röd, liksom den utåtpekande enhetsnormalen $\widehat{\mathbf{n}}$. Den sökta reflekterade strålen är grön, liksom dess sökta normerade riktningsvektor $\widehat{\mathbf{r}}$.

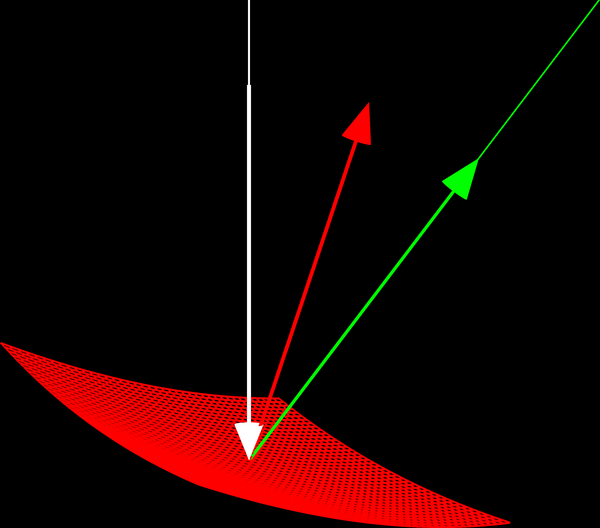
Hur bestämmer vi $\widehat{\mathbf{r}}$ givet $\widehat{\mathbf{i}}$ och $\widehat{\mathbf{n}}$?

Först bestämmer vi (ortogonal)projektionen $\mathbf{p}$ av $\widehat{\mathbf{i}}$ på $\widehat{\mathbf{n}}$; den är

$\mathbf{p}=⟨\widehat{\mathbf{i}}, \widehat{\mathbf{n}}⟩\widehat{\mathbf{n}}$.

Vi söker nu den vektor $\mathbf{x}$ som går från början av $\widehat{\mathbf{i}}$ till normallinjen och som är vinkelrät mot normallinjen (rita!). Tydligen är $\mathbf{x}+\mathbf{p}=\widehat{\mathbf{i}}$ varför

$\mathbf{x}=\widehat{\mathbf{i}}-\mathbf{p}=\widehat{\mathbf{i}}-⟨\widehat{\mathbf{i}}, \widehat{\mathbf{n}}⟩\widehat{\mathbf{n}}$.

Vi hävdar nu att

$\widehat{\mathbf{r}}=-\widehat{\mathbf{i}}+2\mathbf{x}=-\widehat{\mathbf{i}}+2\widehat{\mathbf{i}}-2⟨\widehat{\mathbf{i}}, \widehat{\mathbf{n}}⟩\widehat{\mathbf{n}}=\widehat{\mathbf{i}}-2⟨\widehat{\mathbf{i}}, \widehat{\mathbf{n}}⟩\widehat{\mathbf{n}}$,

enligt bilden nedan, där $\mathbf{p}$ och $\mathbf{x}$ är gula.

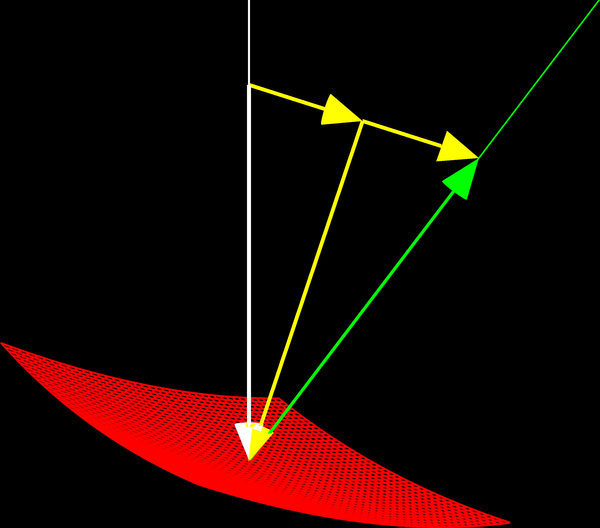
För det första ser vi nämligen att $\widehat{\mathbf{r}}=\widehat{\mathbf{i}}-2⟨\widehat{\mathbf{i}}, \widehat{\mathbf{n}}⟩\widehat{\mathbf{n}}$ är en linjärkombination av $\widehat{\mathbf{i}}$ och $\widehat{\mathbf{n}}$, så att $\widehat{\mathbf{r}}$ ligger i det plan som spänns upp av $\widehat{\mathbf{i}}$ och $\widehat{\mathbf{n}}$. Att sedan infallsvinkeln är lika med reflektionsvinkeln följer direkt av geometrin, med tanke på den likbenta triangel som uppenbarar sig och som består av två kongruenta rätvinkliga trianglar. (Att de två rätvinkliga trianglarna är kongruenta följer av att de gula sidorna intill de räta vinklarna parvis är lika stora i båda trianglarna och det faktum att de är kongruenta medför i sin tur direkt att deras spetiga vinklar, d.v.s. infallsvinkeln och reflektionsvinkeln, är lika stora. Samtidigt följer att $\left|\widehat{\mathbf{i}}\right|=\left|\widehat{\mathbf{r}}\right|$. Det senare faktumet, d.v.s. att den stora triangeln är likbent, följer också av Pythagoras sats applicerad i de två rätvinkliga trianglarna.) Sålunda är $\widehat{\mathbf{r}}$ en riktningsvektor för den reflekterade strålen, enligt reflektionslagen.

Men $\widehat{\mathbf{r}}$ är inte bara en riktningsvektor, utan den utlovade normerade riktningsvektorn, eftersom $\left|\widehat{\mathbf{r}}\right|=\left|\widehat{\mathbf{i}}\right|=1$.

Som en övning i vektoralgebra kan vi utföra några kontroller:

$\mathbf{x}\cdot \widehat{\mathbf{n}}=\left(\widehat{\mathbf{i}}-⟨\widehat{\mathbf{i}}, \widehat{\mathbf{n}}⟩\widehat{\mathbf{n}}\right)\cdot \widehat{\mathbf{n}}=⟨\widehat{\mathbf{i}}, \widehat{\mathbf{n}}⟩-⟨\widehat{\mathbf{i}}, \widehat{\mathbf{n}}⟩{\left|\widehat{\mathbf{n}}\right|}^2=0$,

${\left|\widehat{\mathbf{r}}\right|}^2=\mathbf{r}\cdot \mathbf{r}={\left(\widehat{\mathbf{i}}-2⟨\widehat{\mathbf{i}}, \widehat{\mathbf{n}}⟩\widehat{\mathbf{n}}\right)}^2={\left|\widehat{\mathbf{i}}\right|}^2-4{⟨\widehat{\mathbf{i}}, \widehat{\mathbf{n}}⟩}^2+4{⟨\widehat{\mathbf{i}}, \widehat{\mathbf{n}}⟩}^2{\left|\mathbf{n}\right|}^2=1$ och

$⟨\widehat{\mathbf{r}}, \widehat{\mathbf{n}}⟩=\left(\widehat{\mathbf{i}}-2⟨\widehat{\mathbf{i}}, \widehat{\mathbf{n}}⟩\widehat{\mathbf{n}}\right)\cdot \widehat{\mathbf{n}}=⟨\widehat{\mathbf{i}}, \widehat{\mathbf{n}}⟩-2⟨\widehat{\mathbf{i}}, \widehat{\mathbf{n}}⟩{\left|\widehat{\mathbf{n}}\right|}^2=-⟨\widehat{\mathbf{i}}, \widehat{\mathbf{n}}⟩=⟨-\widehat{\mathbf{i}}, \widehat{\mathbf{n}}⟩$

vilket visar att $\mathbf{x}\perp \widehat{\mathbf{n}}$, $\left|\widehat{\mathbf{r}}\right|=1$ och $\angle \left(\widehat{\mathbf{r}}, \widehat{\mathbf{n}}\right)=\angle \left(-\widehat{\mathbf{i}}, \widehat{\mathbf{n}}\right)$ som förväntat.